
题目列表(包括答案和解析)
7.已知m是平面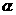 的一条斜线,点
的一条斜线,点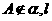 为过点A的一条动直线,那么下列四种情况:
为过点A的一条动直线,那么下列四种情况:
①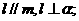 ②
②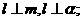 ③
③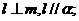 ④
④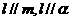 。其中可能出现的种数为
。其中可能出现的种数为
A.0 B.1 C.2 D.3
6.有4名不同科目的实习老师被分配到3个班级,每班至少一人的不同分法有
A.144种 B.72种 C.36种 D.24种
5.已知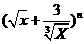 的展开式中各项系数的和与其各项二项式系数的和之比为64,则n
的展开式中各项系数的和与其各项二项式系数的和之比为64,则n
等于
A.4 B.5 C.6 D.7
4.若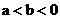 ,则下列不等式中不能成立的是
,则下列不等式中不能成立的是
A.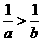 B.
B.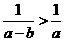 C.
C.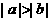 D.
D.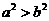
3.若直线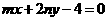 平分圆
平分圆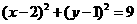 的周长,则
的周长,则 的取值范围是
的取值范围是
A.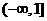 B.
B.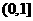 C.
C.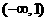 D.(0,1)
D.(0,1)
2.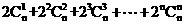 等于
等于
A.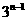 B.
B.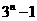 C.
C.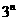 D.
D.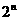
有一项是符合题目要求的。
1.抛物线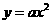 的准线方程是
的准线方程是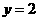 ,则
,则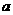 的值为
的值为
A.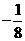 B.
B.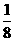 C.8
D.
C.8
D.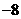
20.(本小题满分10分)已知数列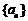 中,
中,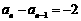 ,
,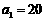 .
.
(1)求数列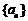 的通项公式
的通项公式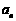 及前
及前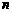 项和
项和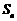 ;(2)求使
;(2)求使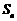 最大的序号
最大的序号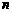 的值.
的值.
(3)求数列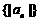 的前
的前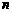 项和
项和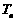 .
.
[解析](1)数列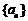 为等差数列,公差
为等差数列,公差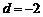 ,
,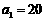
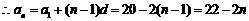 .
.
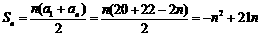 .
.
(2)令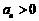 得
得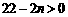 ,
,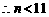 , 令
, 令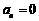 得
得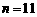 .
.
故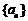 中前10项为正,第11项为零,从第12项开始为负,故使
中前10项为正,第11项为零,从第12项开始为负,故使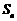 最大的
最大的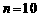 或
或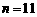 .
.
(3)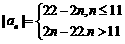
当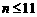 时,
时,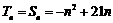 ;
;
当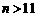 时,
时,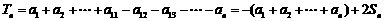
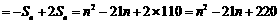
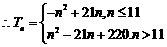


19.(本小题满分8分)已知直线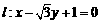 ,一个圆的圆心
,一个圆的圆心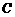 在
在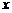 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线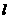 和
和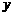 轴均相切.
轴均相切.
(1)求该圆的方程;
(2)直线 :
: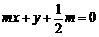 与圆
与圆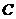 交于
交于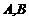 两点,且
两点,且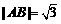 ,求
,求 的值.
的值.
[解析](1)设圆心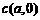 ,
,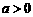 ,半径为
,半径为 ,则
,则
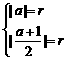
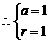
所求圆的方程为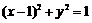 .
.
(2)作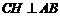 垂足为
垂足为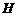 ,则
,则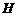 为
为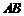 中点
中点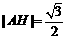 ,
,


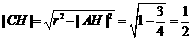 ,即点
,即点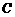 到直线
到直线 的距离为
的距离为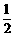 .
.
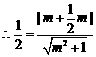
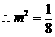 ,
,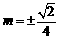 .
.
18.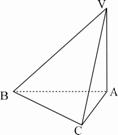 (本小题满分8分)如图,已知三棱锥
(本小题满分8分)如图,已知三棱锥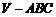 中,
中,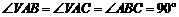 且
且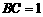 ,
,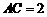 ,
,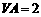 .
.
(1)求证: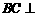 平面
平面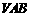 .
.
(2)求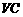 与平面
与平面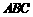 所成的角.
所成的角.
(3)求二面角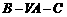 的平面角.
的平面角.
[解析](1)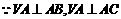 ,
,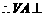 平面
平面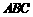
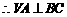 又
又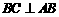
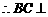 平面
平面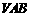 .
.
(2)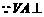 平面
平面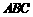
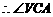 为
为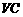 与平面
与平面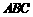 所成的角
所成的角
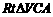 中,
中,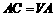

即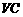 与平面
与平面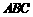 所成的角为
所成的角为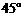 .
.
(3)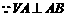 ,
,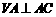
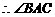 为
为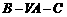 的平面角.
的平面角.
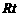
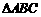 中,
中,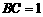 ,
,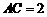

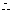 二面角
二面角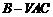 的平面角为
的平面角为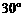 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com