
题目列表(包括答案和解析)
3.现有男、女学生共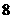 人,从男生中选
人,从男生中选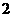 人,从女生中选
人,从女生中选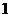 人分别参加数学、物理、化学三科竞赛,共有
人分别参加数学、物理、化学三科竞赛,共有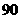 种不同方案,那么男、女生人数分别是( )
种不同方案,那么男、女生人数分别是( )
A.2、6 B. 3、5 C. 5、3 D.6、2
2.已知0<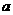 <2,复数z的实部为
<2,复数z的实部为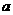 ,虚部为1,则
,虚部为1,则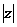 的取值范围是( )
的取值范围是( )
A.(1,5) B.(1,3) C.
(1,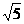 ) D.(1,
) D.(1,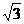 )
)
1.若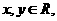 则
则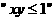 是
是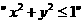 的( )
的( )
A.充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
20.设函数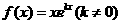
(Ⅰ)求曲线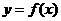 在点
在点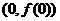 处的切线方程;
处的切线方程;
(Ⅱ)求函数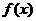 的单调区间;
的单调区间;
(Ⅲ)若函数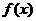 在区间
在区间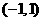 内单调递增,求
内单调递增,求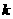 的取值范围.
的取值范围.
19.已知函数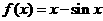 ,数列{
,数列{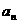 }满足:
}满足: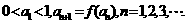
证明:(ⅰ)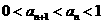 ;(ⅱ)
;(ⅱ)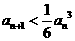 。
。
18.某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区。B肯定是受A感染的。对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是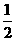 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是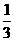 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
17.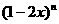 展开式中第6项与第7项的系数的绝对值相等,求展开式中系数最大的项和系数绝对值最大的项.
展开式中第6项与第7项的系数的绝对值相等,求展开式中系数最大的项和系数绝对值最大的项.
16.抛物线y=ax2+bx在第一象限内与直线x+y=4相切.此抛物线与x轴所围成的图形的面积记为S.求使S达到最大值的a、b值,并求Smax.
15.已知某圆的极坐标方程为:ρ2 -4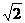 ρcos(θ-
ρcos(θ-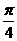 )+6=0.
)+6=0.
(1)将极坐标方程化为普通方程;并选择恰当的参数写出它的参数方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
14.某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第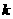 棵树种植在点
棵树种植在点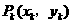 处,其中
处,其中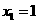 ,
,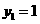 ,当
,当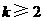 时,
时,
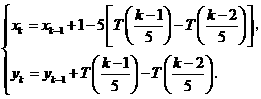
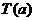 表示非负实数
表示非负实数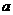 的整数部分,例如
的整数部分,例如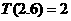 ,
,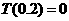 .
.
按此方案,第6棵树种植点的坐标应为 ;第2008棵树种植点的坐标应为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com