
题目列表(包括答案和解析)
1.相关关系的概念
在实际问题中,变量之间的常见关系有两类:
一类是确定性函数关系,变量之间的关系可以用函数表示。例如正方形的面积S与其边长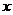 之间的函数关系
之间的函数关系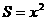 (确定关系);
(确定关系);
一类是相关关系,变量之间有一定的联系,但不能完全用函数来表达。例如一块农田的水稻产量与施肥量的关系(非确定关系)
相关关系:自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
相关关系与函数关系的异同点:
相同点:均是指两个变量的关系。
不同点:函数关系是一种确定关系;而相关关系是一种非确定关系;函数关系是自变量与因变量之间的关系,这种关系是两个非随机变量的关系;而相关关系是非随机变量与随机变量的关系。
1.解析视屏:
2.学法指导:
①求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实标意义.否则,求出的回归直线方程毫无意义.因此,对一组数据作线性回归分析时,应先看其散点图是否成线性.
②求回归直线方程,关键在于正确地求出系数a、b,由于求a、b的计算量较大,计算时仔细谨慎、分层进行,避免因计算产生失误.
③回归直线方程在现实生活与生产中有广泛的应用.应用回归直线方程可以把非确定性问题转化成确定性问题,把“无序”变为“有序”,并对情况进行估测、补充.因此,学过回归直线方程以后,应增强学生应用回归直线方程解决相关实际问题的意识.
[教师在线]
1.学习目标:
了解非确定性关系中两个变量的统计方法;掌握散点图的画法及在统计中的作用,掌握
回归直线方程的求解方法。
8.三角形的一边长为14,这条边所对的角为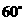 ,另两边之比为8:5,则这个三角形的
,另两边之比为8:5,则这个三角形的
面积为 。
9在△ABC中,已知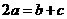 ,
,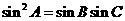 ,试判断△ABC的形状。
,试判断△ABC的形状。
10在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足:
2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积。
7.在钝角△ABC中,已知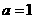 ,
,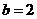 ,则最大边
,则最大边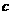 的取值范围是
。
的取值范围是
。
6.在△ABC中,已知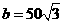 ,
,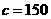 ,
,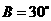 ,则边长
,则边长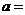 。
。
5.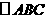 中,
中,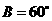 ,
,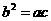 ,则
,则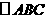 一定是
( )
一定是
( )
A 锐角三角形 B 钝角三角形 C 等腰三角形 D 等边三角形
4.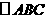 中,
中,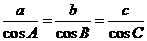 ,则
,则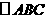 一定是
( )
一定是
( )
A 直角三角形 B 钝角三角形 C 等腰三角形 D 等边三角形
3.长为5、7、8的三角形的最大角与最小角之和为 ( )
A 90° B 120° C 135° D 150°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com