
题目列表(包括答案和解析)
4. 随机变量X的分布列如右表,则X的数学
期望是( A )
A. 2.2 B. 2.1 C. 2.0 D. 随m的变化而变化
3、已知命题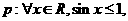 则
则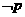 是
( )
是
( )
A、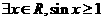 B、
B、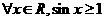
C、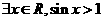 D、
D、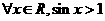
|
X |
1 |
2 |
3 |
|
P |
0.2 |
0.4 |
m |
2、如果双曲线的半实轴长为2,焦距为6,那么该双曲线的离心率是 ( )
A、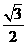 B、
B、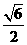 C、
C、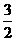 D、2
D、2
1、向量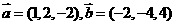 ,则
,则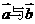 ( )
( )
A、相交 B、垂直 C、平行 D、以上都不对
20.(本题满分14分).
等差数列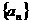 中,
中,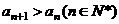 ,
,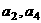 为方程
为方程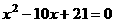 的两根,前
的两根,前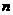 项和为
项和为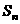 .等比数列
.等比数列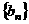 的前
的前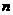 项和
项和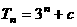 (
(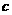 为常数).
为常数).
(I)求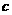 ;
;
(II)证明:对任意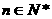 ,
,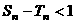 ;
;
(III)证明:对任意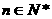 ,
,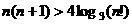 .
.
19.(本小题满分14分)
如图,四面体ABCD中,O、E分别是BD、BC的中点, ,
,
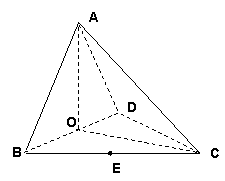
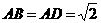
(Ⅰ)求证: 平面BCD;
平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离.
18. (本小题满分14分)
已知函数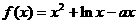 在
在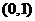 上是增函数。
上是增函数。
(Ⅰ)求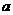 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设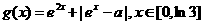 ,求函数
,求函数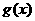 的最小值。
的最小值。
17.(本小题满分14分)
设椭圆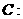
 的离心率为
的离心率为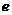 =
=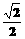 ,点
,点 是椭圆上的一点,且点
是椭圆上的一点,且点 到椭圆
到椭圆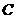 两焦点的距离之和为4.
两焦点的距离之和为4.
(Ⅰ)求椭圆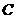 的方程;
的方程;
(Ⅱ)椭圆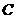 上一动点
上一动点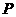
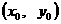 关于直线
关于直线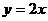 的对称点为
的对称点为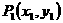 ,求
,求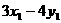 的取值范围.
的取值范围.
16.(本题满分12分)
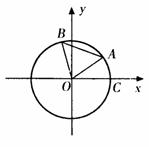
如图点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴
的交点,△AOB是正三角形,若点A的坐标为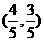 ,记∠COA=α。
,记∠COA=α。
 (Ⅰ)求
(Ⅰ)求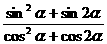 的值;
的值;
(Ⅱ)求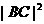 的值。
的值。
15.(本小题满分12分)
某学生答对A、B、C三个不同试题的概率分别是0.4,0.5,0.6,且学生答对三道试题是互不 影响,设X表示学生答对题目数与没有答对题目数差的绝对值。
(Ⅰ)求X的分布列及均值;
(Ⅱ)记“函数f(x)=x2-3Xx+1在区间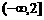 上单调递减”为事件A,求事件A的概率.
上单调递减”为事件A,求事件A的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com