
题目列表(包括答案和解析)
1.下列函数在其定义域上不是连续函数的是( )
A.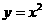 B.
B.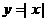 C.
C.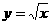 D.
D.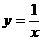
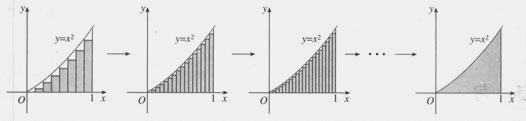
2、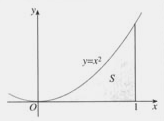 思考:如何求上述图形的面积?它与直边图形的主要区别是什么?能否将求这个图形的面积转化为求直边图形的面积问题?
思考:如何求上述图形的面积?它与直边图形的主要区别是什么?能否将求这个图形的面积转化为求直边图形的面积问题?
例1、求由抛物线y=x2与x轴及x=1所围成的平面图形的面积S.
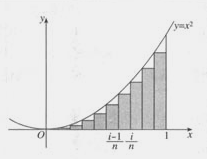
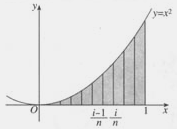 分析:我们发现曲边图形与“直边图形”的主要区别是,曲边图形有一边是 线段,而“直边图形”的所有边都是 线段。我们可以采用“以直代曲,逼近”的思想得到解决问题的思路:将求曲边梯形面积的问题转化为求“直边图形”面积的问题.
分析:我们发现曲边图形与“直边图形”的主要区别是,曲边图形有一边是 线段,而“直边图形”的所有边都是 线段。我们可以采用“以直代曲,逼近”的思想得到解决问题的思路:将求曲边梯形面积的问题转化为求“直边图形”面积的问题.
解:(1)分割(化整为零)
 将区间
将区间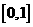 等分成
等分成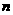 个小区间
个小区间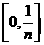 ,
,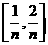 ,… 则第i个小区间为
(i=1,2,…,
,… 则第i个小区间为
(i=1,2,…,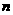 ),第
),第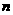 个小区间为
,每个区间的长度为
个小区间为
,每个区间的长度为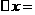 = ,过各个区间端点作
= ,过各个区间端点作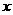 轴的垂线,从而得到
轴的垂线,从而得到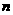 个小曲边梯形,它们的面积分别记作
个小曲边梯形,它们的面积分别记作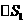 ,
,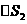 ,…,
,…,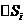 ,…,
,…,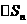 .显然,S=
.
.显然,S=
.
(2)近似代替 (以不变高代替变高,以矩形代替曲边梯形)
对区间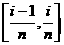 上的小曲边梯形,以区间左端点对应的函数值
上的小曲边梯形,以区间左端点对应的函数值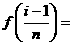 为一边的长,以
为一边的长,以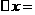 为邻边的长的小矩形的面积近似代替小曲边梯形的面积,即
为邻边的长的小矩形的面积近似代替小曲边梯形的面积,即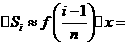 (i=1,2,…,
(i=1,2,…,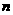 ).
).
(3)求和(积零为整,给出“整”的近似值)
因为每个小矩形的面积是相应的小曲边梯形面积的近似值,所以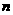 个小矩形面积之和就是所求曲边三角形面积
个小矩形面积之和就是所求曲边三角形面积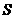 的近似值:
的近似值:
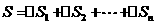
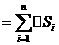 = = = .
= = = .
(4)取极限
当分割无限变细时,即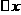 无限趋近于
无限趋近于 (
(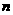 趋向于
趋向于 )
)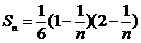 趋向于 ,从而有S=
.
趋向于 ,从而有S=
.
变式拓展:求直线x=0,x=2,y=0与曲线y=x2所围成的曲边梯形的面积.
反思:
例2:一辆汽车在笔直的公路上变速行使,设汽车在时刻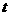 的速度为
的速度为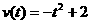 (单位
(单位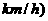 ,求它在
,求它在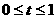 (单位:
(单位: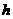 )这段时间内行使的路程
)这段时间内行使的路程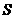 (单位:
(单位: ).
).
探究P49
变式拓展:一辆汽车在笔直的公路上变速行使,设汽车在时刻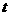 的速度为
的速度为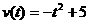 (单位
(单位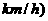 ,求它在
,求它在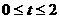 (单位:
(单位: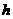 )这段时间内行使的路程
)这段时间内行使的路程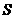 (单位:
(单位: ).
).
反思:
1、概念:如图,由直线x=a , x= b , x轴,曲线y=f (x)所围成的图形称为 .
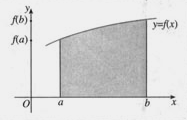 探求、讨论、体会以直代曲数学思想.
探求、讨论、体会以直代曲数学思想.
2、匀速直线运动的时间(t)、速度(v)与路程(S)的关系 .
1、直边图形的面积公式:三角形 ,矩形 ,梯形 ;
重点:求曲边梯形的面积、汽车行驶的路程;
难点:深入理解“分割、近似代替、求和、求极限”的思想.
1.通过对曲边梯形面积的探求,掌握好求曲边梯形的面积的四个步骤-分割、近似代替、求和、求极限;
2 通过求曲边梯形的面积、变速运动中的路程,初步了解定积分产生的背景.
通过求曲边梯形的面积、变速运动中的路程,初步了解定积分产生的背景.
20.解析:证法一:由正弦定理: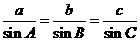 得
得
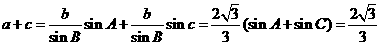
[sinA+sin(120°-A)]=2sin(A+30°)
∵0°<A<120°,∴30°<A+30°<150° ∴1<2sin(A+30°)≤2.
证法二 ∵B=60°,b=1,∴a2+c2-b2=2accos60° ∴a2+c2-1=ac,∴a2+c2-ac=1,∴(a+c)2+3(a-c)2=4 ∴(a+c)2=4-3(a-c)2,∵0≤a-c<1 ∴0≤3(a-c)2<3,∴4-3(a-c)2≤4 即(a+c)2≤4,∴a+c≤2, 又a+c>1 ∴1<a+c≤2.
20.在△ABC中, A、B、C成等差数列,b=1,求证:1<a+c≤2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com