
题目列表(包括答案和解析)
2. 正弦定理与三角形的外接圆紧密联系,它们之间的具体关系是怎样的?
解析:设三角形ABC的外接圆的半径为R,外接圆圆心为O,则有: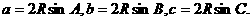 具体的证明如下:
具体的证明如下:
在下图中,连接CO延长后交圆O于A ,则A
,则A C=2R,连接A
C=2R,连接A B,则
B,则
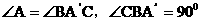 。在
。在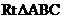 中,BC=a,所以
中,BC=a,所以
a=2Rsin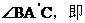 a=2RsinA .同理可得:b=2RsinB,c=2RsinC.即:
a=2RsinA .同理可得:b=2RsinB,c=2RsinC.即: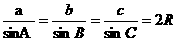 。
。
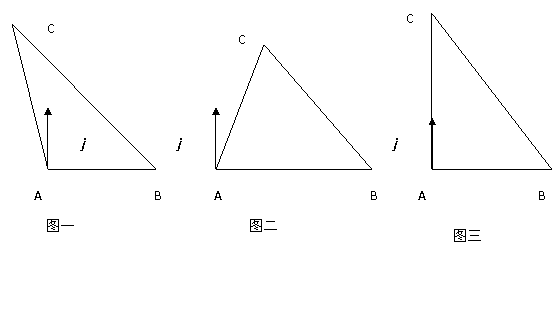
1. 正弦定理除了课本上用几何的方法证明外,和可以用向量的方法进行证明,下面我们以钝角三角形为例进行说明.
解析:在钝角三级形ABC中,如图一中,过A做单位向量j 垂直于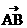 ,则向量j与
,则向量j与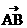 为
为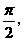 向量j与
向量j与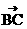 的夹角为
的夹角为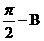 ,向量j与
,向量j与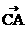 的夹角为
的夹角为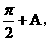 设AB=c,BC=a,AC=b.因为
设AB=c,BC=a,AC=b.因为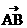 +
+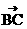 +
+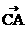 =0,所以j(
=0,所以j(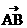 +
+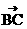 +
+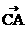 )=j
)=j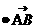 + j
+ j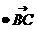 + j
+ j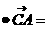 0。
0。
即 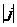
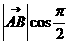 +
+ 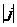
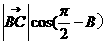 +
+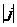
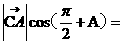 0.
0.
所以

当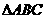 为锐角三角形(图二),直角三角形(图三)时,利用同样的方法证得结论。
为锐角三角形(图二),直角三角形(图三)时,利用同样的方法证得结论。
3.用正弦定理可解决下列那种问题
① 已知三角形三边;②已知三角形两边与其中一边的对角;③已知三角形两边与第三边的对角;④已知三角形三个内角;⑤已知三角形两角与任一边;⑥已知三角形一个内角与它所对边之外的两边。
诱思探究:
2.一般地,把三角形的三个角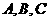 和它们所对的边
和它们所对的边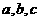 叫做三角形的 ,已知三角形的几个元素求其它元素的过程叫做
。
叫做三角形的 ,已知三角形的几个元素求其它元素的过程叫做
。
1.正弦定理 在一个三角形中,各边和它所对角的_______的比相等,即_______。
3.能够运用正弦定理解决某些与测量和几何有关的实际问题。
情境导入:

2008年青岛奥帆赛成功举办,在比赛中千百艘帆船如离弦之“箭”射向终点,我们知道帆船航行的动力来源于风力,风对帆船的动力与帆船上成三角形的帆布有直接关系, 那我们怎样借助于数学知识设计出比较好的帆船呢?
新知导学:
2.掌握正弦定理,能初步运用正弦定理解一些斜三角形;
1.在已有知识的基础上,通过对任意三角形边角关系的探究,发现并掌握三角形中的边长与角度之间的数量关系-正弦定理。
1.1 正弦定理和余弦定理
课标导读:
6.甲乙两地生产某种产品,它们可以调出的数量分别为300吨,750吨。A、B、C三地需要该产品数量分别为200吨、450吨、400吨,甲地运往A、B、C三地的费用分别为6元/吨,3元/吨,5元/吨,乙地运往A、B、C三地的费用分别为5元/吨、9元/吨、6元/吨,问怎样调运,才能使总运费最小?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com