
题目列表(包括答案和解析)
4.正常情况下,年龄在18岁到38岁的人们,体重y(kg)依身高x(cm)的回归方程为y=0.72x-58.5。张红红同学不胖不瘦,身高1米78,他的体重应在 kg左右。
3.设有一个回归方程为y=2-1.5x,则变量x每增加一个单位时,y平均 ( )
A.增加1.5单位 B.增加2单位 C.减少1.5单位 D.减少2单位
2.某市纺织工人的月工资(元)依劳动生产率(千元)变化的回归方程为y=50+80x,则下列说法中正确的是 ( )
A.劳动生产率为1000元时,月工资为130元
B.劳动生产率提高1000元时,月工资提高约为130元
C.劳动生产率提高1000元时,月工资提高约为80元
D.月工资为210元时,劳动生产率为2000元
1. 下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的余弦值 B.正方形边长和面积
C.正n边形的边数和它的内角和 D.人的年龄和身高
2.经典回放:
例1:下列各组变量哪个是函数关系,哪个是相关关系?
(1)电压U与电流I
(2)圆面积S与半径R
(3)自由落体运动中位移s与时间t
(4)粮食产量与施肥量
(5)人的身高与体重
(6)广告费支出与商品销售额
分析:函数关系是一种确定关系;而相关关系是一种非确定关系;函数关系是自变量与因变量之间的关系,这种关系是两个非随机变量的关系;而相关关系是非随机变量与随机变量的关系。
解:前三小题中一个变量的变化可以确定另一个变量的变化,两者之间是函数关系。
对于粮食与施肥量,两者确实有非常密切的关系,实践证明,在一定的范围内,施肥量越多,粮食产量就越高,但是,施肥量并不能完全确定粮食产量,因为粮食产量还与其他因素的影响有关,如降雨量、田间管理水平等。因此,粮食与施肥量之间不存在确定的函数关系。
人的身高与人的体重也密切相关,一般来说,一个人的身高越高,体重也越重,但同样身高的人,其体重不一定相同,身高和体重这两个变量之间并不是严格的函数关系。
广告费支出与商品销售额有密切的关系,但广告费的支出不能完全决定商品的销售额。由此可见,后三小题各对变量之间的关系是相关关系。
点评:不要认为两个变量间除了函数关系,就是相关关系,事实是上,两个变量间可能毫无关系。比如地球运行的速度与某个人的行走速度就可认为没有关系。
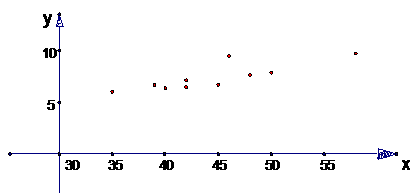
例2:已知10只狗的血球体积及红血球的测量值如下:
|
x |
45 |
42 |
46 |
48 |
42 |
35 |
58 |
40 |
39 |
50 |
|
y |
6.53 |
6.30 |
9.25 |
7.50 |
6.99 |
5.90 |
9.49 |
6.20 |
6.55 |
7.72 |
x(血球体积,mm),y(血红球数,百万)
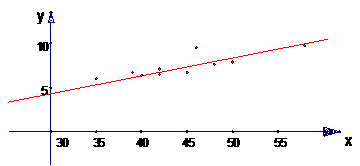
(1)画出上表的散点图;(2)求出回归直线并且画出图形。
解:(1)见下图
(2)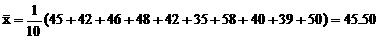
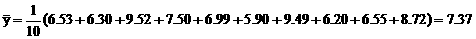
设回归直线为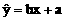 ,
,
则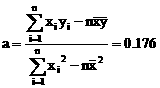 ,
,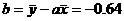
所以所求回归直线的方程为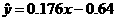 ,图形如下:
,图形如下:
点评:对一组数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数a、b的计算公式,算出a、b.由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误.求线性回归方程的步骤:计算平均数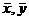 ;计算
;计算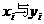 的积,求
的积,求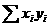 ;计算
;计算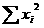 ;将结果代入公式求a;用
;将结果代入公式求a;用 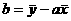 求b;写出回归方程。
求b;写出回归方程。
[同步训练]
2.求回归直线方程的思想方法
观察散点图的特征,发现各点大致分布在一条直线的附近,思考:类似图中的直线可画几条?
引导学生分析,最能代表变量x与y之间关系的直线的特征:即n个偏差的平方和最小,其过程简要分析如下:
设所求的直线方程为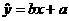 ,其中a、b是待定系数。
,其中a、b是待定系数。
则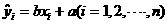 ,于是得到各个偏差。
,于是得到各个偏差。
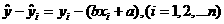
显见,偏差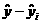 的符号有正负,若将它们相加会造成相互抵消,所以它们的和不能代表几个点与相应直线在整体上的接近程度,故采用n个偏差的平方和
的符号有正负,若将它们相加会造成相互抵消,所以它们的和不能代表几个点与相应直线在整体上的接近程度,故采用n个偏差的平方和
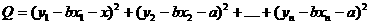
表示n个点与相应直线在整体上的接近程度。
记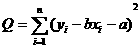 。
。
上述式子展开后,是一个关于a,b的二次多项式,应用配方法,可求出使Q为最小值时的a,b的值,即
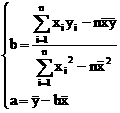
其中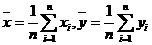
以上方法称为最小二乘法。
1.相关关系的概念
在实际问题中,变量之间的常见关系有两类:
一类是确定性函数关系,变量之间的关系可以用函数表示。例如正方形的面积S与其边长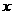 之间的函数关系
之间的函数关系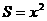 (确定关系);
(确定关系);
一类是相关关系,变量之间有一定的联系,但不能完全用函数来表达。例如一块农田的水稻产量与施肥量的关系(非确定关系)
相关关系:自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系。
相关关系与函数关系的异同点:
相同点:均是指两个变量的关系。
不同点:函数关系是一种确定关系;而相关关系是一种非确定关系;函数关系是自变量与因变量之间的关系,这种关系是两个非随机变量的关系;而相关关系是非随机变量与随机变量的关系。
1.解析视屏:
2.学法指导:
①求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实标意义.否则,求出的回归直线方程毫无意义.因此,对一组数据作线性回归分析时,应先看其散点图是否成线性.
②求回归直线方程,关键在于正确地求出系数a、b,由于求a、b的计算量较大,计算时仔细谨慎、分层进行,避免因计算产生失误.
③回归直线方程在现实生活与生产中有广泛的应用.应用回归直线方程可以把非确定性问题转化成确定性问题,把“无序”变为“有序”,并对情况进行估测、补充.因此,学过回归直线方程以后,应增强学生应用回归直线方程解决相关实际问题的意识.
[教师在线]
1.学习目标:
了解非确定性关系中两个变量的统计方法;掌握散点图的画法及在统计中的作用,掌握
回归直线方程的求解方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com