
题目列表(包括答案和解析)
6.设函数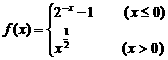 若
若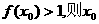 的取值范围是 ( )
的取值范围是 ( )
A.(-1,1) B.(-1,+∞)
C. D.
D.
5.已知: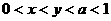 则有 ( )
则有 ( )
A.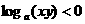 B.
B.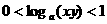
C.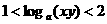 D.
D.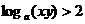
4.已知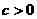 ,设p:函数
,设p:函数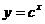 在R上单调递减。
在R上单调递减。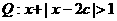 不等式的解集为R。
不等式的解集为R。
如果p和Q有且仅有一个正确,求c的取值范围 ( )
A.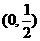 B.
B.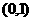 C.
C.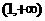 D.
D.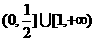
3.函数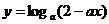 在[0,1]上是减函数,则a的取值范围 ( )
在[0,1]上是减函数,则a的取值范围 ( )
A.(0,1) B.(1,2) C.(0,2) D.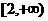
2.设偶函数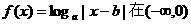 上递增函数,则
上递增函数,则 的大小关系
的大小关系
是 ( )
A.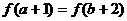 B.
B.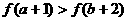
C.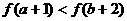 D.不确定
D.不确定
1.设函数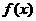 满足
满足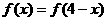 且当
且当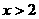 时,
时,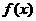 是增函数,则
是增函数,则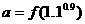
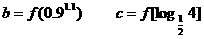 的大小关系是 ( )
的大小关系是 ( )
A.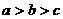 B.
B.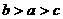 C.
C.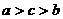 D.
D.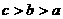
20.(本小题满分14分)
设数列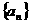 是以a为首项,q为公比的等比数列,令
是以a为首项,q为公比的等比数列,令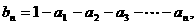
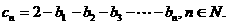
(Ⅰ)试用a,q表示bn和cn;
(Ⅱ)若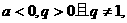 试比较
试比较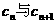 的大小;
的大小;
(Ⅲ)是否存在实数对(a,q),其中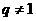 ,使
,使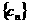 成等比数列,若存在,求出实数对(a,q)和
成等比数列,若存在,求出实数对(a,q)和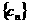 ;若不存在,请说明理由.
;若不存在,请说明理由.
北京市东城区2004年高三年级综合练习(一)
19.(本小题满分14分)
已知椭圆C的中心在原点,左焦点为F1,其右焦点F2和右准线分别是抛物线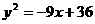 的顶点和准线.
的顶点和准线.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若点P为椭圆C上的一个动点,当∠F1PF2为钝角时,求点P横坐标的取值范围.
18.(本小题满分14分)
为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元.若总用电量为S千瓦时,设高峰时段用电量为x千瓦时.
(Ⅰ)写出实行峰谷电价的电费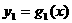 及现行电价的电费
及现行电价的电费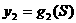 的函数解析式及电费总差额
的函数解析式及电费总差额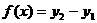 的解析式;
的解析式;
(Ⅱ)对于用电量按时均等的电器(在任何相同的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?
(Ⅲ)你认为每家每户是否都适合“峰谷电价”的计费方法?(只回答是或不是)
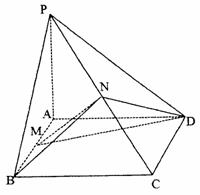
17.(本小题满分14分)
已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.
(Ⅰ)求证:MN⊥AB;
(Ⅱ)若平面PCD与平面ABCD所成的二面角为45°,且PD=AB,求证:平面MND⊥平面PCD;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥N-AMD的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com