
题目列表(包括答案和解析)
10.函数f(x)=sin2x+5sin(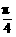 +x)+3的最小值是
+x)+3的最小值是
A.-3 B.-6 C.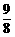 D.-1
D.-1
解析:f(x)=2sinxcosx+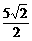 (sinx+cosx)+3.令t=sinx+cosx,t∈[-
(sinx+cosx)+3.令t=sinx+cosx,t∈[-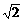 ,
,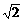 ],则y=(t+
],则y=(t+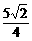 )2-
)2-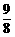 .则当t=-
.则当t=-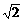 时,ymin=-1,选D.
时,ymin=-1,选D.
答案:D
9.已知f(sinx)=sin3x,则f(cosx)等于
A.-cos3x B.cos3x C.sin3x D.-sin3x
解析:f(cosx)=f[sin(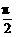 -x)]=sin3(
-x)]=sin3(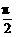 -x)=-cos3x,选A.
-x)=-cos3x,选A.
答案:A
8. 的值是
的值是
A.-3 B.2 C.-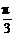 D.
D.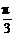
解析:原式=-3,选A.
答案:A
7.方程cosx=lgx的实根个数为
A.1个 B.2个 C.3个 D.无数个
解析:当x=10时,lgx=1,在同一坐标系中画出y=cosx和y=lgx的图象,可知有3个交点,选C.
答案:C
6.在△ABC中,tanA·tanB>1,则△ABC为
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰三角形
解析:tan(A+B)=-tanC,得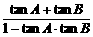 =-tanC.∵tanA·tanB>1,∴tanA>0,tanB>0.1-tanA·tanB<0,∴-tanC<0.tanC>0,∴△ABC为锐角三角形.故选B.
=-tanC.∵tanA·tanB>1,∴tanA>0,tanB>0.1-tanA·tanB<0,∴-tanC<0.tanC>0,∴△ABC为锐角三角形.故选B.
答案:B
5.y=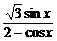 的值域是
的值域是
A.[-1,1] B.[-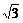 ,
,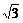 ]
]
C.[-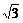 ,1] D.[-1,
,1] D.[-1,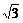 ]
]
解析:原式可化为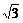 sinx+ycosx=2y,
sinx+ycosx=2y,
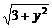 sin(x+
sin(x+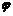 )=2y(tan
)=2y(tan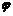 =
=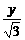 ),
),
sin(x+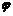 )=
)=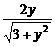 ∈[-1,1],
∈[-1,1],
解得y∈[-1,1].
答案:A
4.设集合M={y|y=sinx},N={y|y=cosxtanx},则M、N的关系是
A.N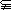 M B.M
M B.M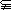 N C.M=N D.M∩N=
N C.M=N D.M∩N=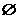
解析:M={y|-1≤y≤1},N={y|-1<y<1},选A.
答案:A
3.已知函数y=Asin(ωx+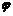 )在同一周期内,当x=
)在同一周期内,当x=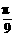 时,取得最大值
时,取得最大值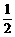 ,当x=
,当x=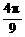 时,取得最小值-
时,取得最小值-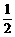 ,则该函数的解析式为
,则该函数的解析式为
A.y=2sin(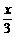 -
-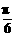 ) B.y=
) B.y=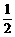 sin(3x+
sin(3x+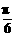 )
)
C.y=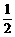 sin(3x-
sin(3x-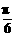 ) D.y=
) D.y=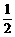 sin(
sin(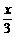 -
-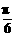 )
)
解析:A=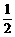 ,
,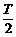 =
=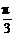 ,ω=
,ω=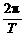 =3,易知第一个零点为(-
=3,易知第一个零点为(-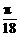 ,0),则y=
,0),则y=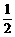 sin[3(x+
sin[3(x+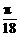 )],即y=
)],即y=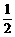 sin(3x+
sin(3x+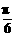 ).
).
答案:B
2.要得到函数y=sin2x的图象可由函数y=cos2x的图象
A.向左平移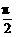 个单位 B.向右平移
个单位 B.向右平移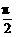 个单位
个单位
C.向左平移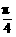 个单位 D.向右平移
个单位 D.向右平移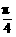 个单位
个单位
解析:y=sin2x=cos(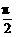 -2x)=cos[2(x-
-2x)=cos[2(x-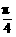 )].
)].
答案:D
1.(2004年辽宁,1)若cosθ>0,且sin2θ<0,则角θ的终边所在象限是
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:由sin2θ<0得2sinθcosθ<0.又cosθ>0,∴sinθ<0.∴角θ的终边在第四象限.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com