
题目列表(包括答案和解析)
1.在等差数列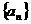 中,已知前20项之和
中,已知前20项之和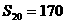 ,则
,则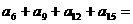 ( )
( )
A. 34 B. 51 C. 68 D. 70
23.(本题满分14分)已知曲线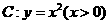 ,过
,过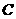 上的点
上的点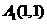 作曲线
作曲线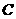 的切线
的切线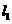 交
交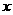 轴于点
轴于点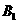 ,再过点
,再过点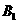 作
作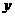 轴的平行线交曲线
轴的平行线交曲线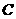 于点
于点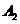 ,再过点
,再过点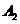 作曲线
作曲线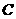 的切线
的切线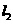 交
交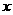 轴于点
轴于点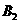 ,再过点
,再过点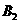 作
作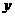 轴的平行线交曲线
轴的平行线交曲线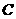 于点
于点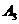 ,……,依次作下去,记点
,……,依次作下去,记点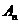 的横坐标为
的横坐标为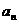
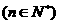
(1)求数列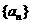 的通项公式;(2)设数列
的通项公式;(2)设数列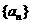 的前
的前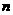 项和为
项和为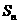 ,求证:
,求证: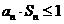
(3)求证: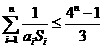
22.(本题满分14分)已知点A(-2,0)、B(2,0),动点C在x轴上的射影为点D,且满足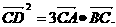
(1)求动点C的轨迹E的方程;
(2)若P、Q为轨迹E上的不同两点,且满足PA⊥QA ,试问直线PQ是否恒过一个定点?若是,则求出该定点坐标;若不是,请说明理由。
19.(本小题满分14分)
已知函数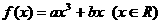 ,
,
(1)若函数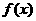 的图象在点
的图象在点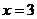 处的切线与直线
处的切线与直线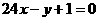 平行,函数
平行,函数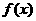 在
在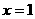 处取得极值,求函数
处取得极值,求函数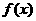 的解析式,并确定函数的单调递减区间;
的解析式,并确定函数的单调递减区间;
(2)若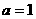 ,且函数
,且函数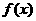 在
在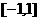 上是减函数,求
上是减函数,求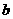 的取值范围。(浙理)
的取值范围。(浙理)
(19)(本小题满分12分,每小问满分4分)
已知某地区人口数量较大,经检测有5%的男人、1%的女人是色盲,假设该地区男女各占一半。
(1)随机挑选一人,求此人恰是色盲的概率;
(2)随机挑选三人,恰有两人恰是色盲的概率。
(3)该地区有一所中学,男生200人、女生100人,现从中任意抽取男生、女生各5名进行体检,发现色盲的概率有多大?(用算式表示即可)。
17.(本题满分14分)如图,四棱锥P -ABCD的底面是矩形,侧面PAD是 正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
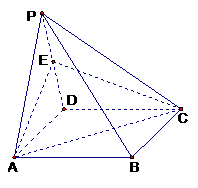 (1)求证:直线PB与平面EAC的关系;
(1)求证:直线PB与平面EAC的关系;
(2)求证:AE⊥平面PCD;
(3)若AD = AB,试求二面角A-PC-D的正切值;
(4)当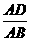 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
(21) (本小题满分14分,第一小问满分6分,第二小问满分8分)
已知函数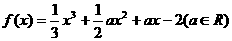
(Ⅰ)若函数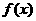 在区间(-∞,+∞)上为单调函数,求实数a的取值范围;
在区间(-∞,+∞)上为单调函数,求实数a的取值范围;
(Ⅱ)设A(x1,
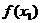 )、B(x2,
)、B(x2, 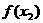 )是函数
)是函数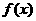 的两个极值点,若直线AB的斜率不小于
的两个极值点,若直线AB的斜率不小于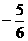 ,求实数a的取值范围。
,求实数a的取值范围。
18.若函数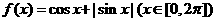 的图象与直线
的图象与直线 有且仅有四个不同的交点,则
有且仅有四个不同的交点,则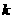 的取值范围是__________
的取值范围是__________
17.已知椭圆 与双曲线
与双曲线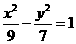 在第一象限内的交点为
在第一象限内的交点为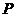 ,则点
,则点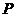 到椭圆右焦点的距离等于______
到椭圆右焦点的距离等于______
16.在△ABC中,a、b、c分别是∠A、∠B、∠C所对的边。若∠B =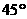 ,b=2
,b=2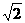 ,c=2,则∠A=
.
,c=2,则∠A=
.
15.已知函数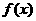 =则
=则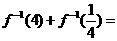 .
.
14.已知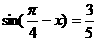 ,则
,则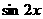 的值为_____________
的值为_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com