
题目列表(包括答案和解析)
3、将7名学生分配到甲、乙两个宿舍中, 每个宿舍至少安排2名学生, 那么互不相同的分配方案共有_112 __ 种.
2、某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是_ 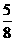 _.
_.
1、一人口袋里装有大小相同的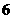 个小球,其中红色、黄色、绿色的球各
个小球,其中红色、黄色、绿色的球各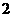 个。如果任意取出
个。如果任意取出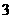 个小球,那么其中恰有
个小球,那么其中恰有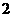 个小球同颜色的概率是
个小球同颜色的概率是 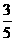 (用分数表示)。
(用分数表示)。
22、 已知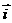 ,
,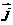 分别是与x轴、y轴正方向相同的单位向量,
分别是与x轴、y轴正方向相同的单位向量,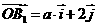
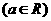 ,对任意正整数n,
,对任意正整数n,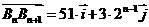 。
。
(1)若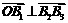 ,求a的值;
,求a的值;
(2)求向量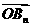 ;
;
(3)设向量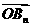
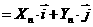 ,求最大整数a的值,使对任意正整数n,都有
,求最大整数a的值,使对任意正整数n,都有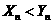 成立。
成立。
2006届闵行三中高三期末强化卷(四)
21、已知函数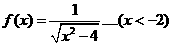
(1)求f(x)的反函数f-1(x);
(2)设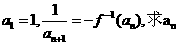
(3)设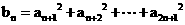 ,是否存在最小正整数m,使对任意
,是否存在最小正整数m,使对任意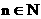 ,都有
,都有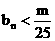 成立?若存在,求出m的值,若不存在说明理由。
成立?若存在,求出m的值,若不存在说明理由。
20、.数列{an}满足an=3an-1+3n-1 (n³2),且a3=95。
(1) 求a1,a2;
(2) 是否存在一个实数t,使得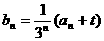 (nÎZ+),{bn}为等差数列。有,则求出t,并予以证明;没有,则说明理由;
(nÎZ+),{bn}为等差数列。有,则求出t,并予以证明;没有,则说明理由;
(3) 求数列{an}的前n项和Sn。
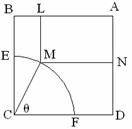
19、如图,某小区有一块边长为50米的正方形空地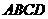 ,其中
,其中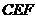 是一个以
是一个以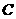 为圆心,
为圆心, 为半径的扇形,
为半径的扇形,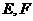 分别在
分别在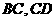 上,在此拟建水池与人行道;
上,在此拟建水池与人行道;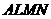 为一矩形,
为一矩形,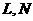 分别在
分别在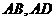 上,
上,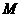 在弧
在弧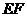 上,在此拟建活动中心;其余部分为绿化区域,设
上,在此拟建活动中心;其余部分为绿化区域,设 =
=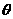 ,绿化区域的面积为
,绿化区域的面积为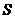 。
。
 (1)当
(1)当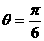 时,求
时,求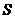 关于
关于 的函数解析式
的函数解析式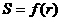 ,并求当
,并求当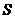 取最大值时相应的
取最大值时相应的 的值(精确到0.001);
的值(精确到0.001);
(2)当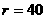 米时,求
米时,求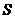 的最大值(精确到0.001)。
的最大值(精确到0.001)。
18、设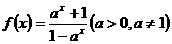
(1)求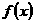 的反函数
的反函数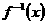 :
:
(2)讨论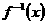 在
在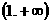 上的单调性,并加以证明:
上的单调性,并加以证明:
(3)令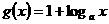 ,当
,当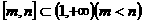 时,
时,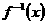 在
在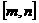 上的值域是
上的值域是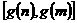 ,求
,求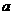 的取值范围。
的取值范围。
17、命题甲: 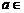 R, 关于x的方程
R, 关于x的方程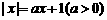 有两个非零实数解;
有两个非零实数解;
命题乙: 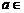 R, 关于x的不等式
R, 关于x的不等式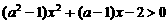 的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
的解集为空集; 当甲、乙中有且仅有一个为真命题时, 求实数a的取值范围.
16、已知: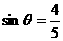 ,且
,且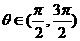 求
求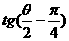 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com