
题目列表(包括答案和解析)
3、设函数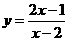 ,则下列命题正确的是(
)
,则下列命题正确的是(
)
①图象上一定存在两点它们的连线平行于x轴。②图象上任意两点的连线都不平行于y轴。③图象关于直线y=x对称。④图象关于原点对称。
A ①③ B ②③ C ②④ D ③
2、f(x)是定义在R上的奇函数,它的最小正周期是T,则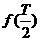 的值是( )
的值是( )
A 0 B
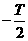 C
C 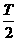 D 无法确定
D 无法确定
1、设集合E=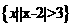 ,F=
,F=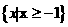 ,则
,则 ( )
( )
A. 充分不必要条件B必要不充分条件 C 充要条件 D不充分不必要条件
17 (本小题满分12分)
已知等比数列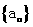 中,
中,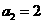 ,
,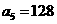 .
.
(I) 求通项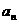 ;
;
(II) 若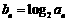 ,
,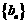 数列的前
数列的前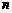 项和为
项和为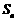 ,且
,且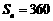 ,求
,求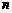 的值.
的值.
18 (本小题满分12分)
从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试 每个甲品牌元件能通过测试的概率均为
每个甲品牌元件能通过测试的概率均为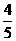 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为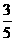
 试求:
试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率;
(II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率
19 (本小题满分12分)
已知向量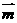 =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量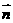 =(2,0)的夹角为
=(2,0)的夹角为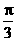 ,其中A, B, C是
,其中A, B, C是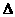 ABC的内角.
ABC的内角.
(I)求角B的大小; (II)求sinA+sinC的取值范围.
20 (本小题满分12分)
已知函数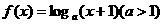 ,若函数
,若函数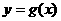 图象上任意一点P关于原点的对称点Q的轨迹恰好是函数
图象上任意一点P关于原点的对称点Q的轨迹恰好是函数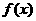 的图象
的图象
(1)写出函数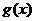 的解析式;
的解析式;
(2)当 时,总有
时,总有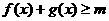 成立,求实数
成立,求实数 的取值范围
的取值范围
21 (本小题满分12分)
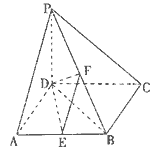
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
(1)求证:EF⊥CD;
(2)求DB与平面DEF所成角的大小;
(3)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论
22 (本小题满分14分)
设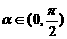 ,函数
,函数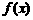 的定义域为
的定义域为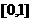 ,且
,且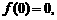
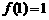 ,对定义域内任意的
,对定义域内任意的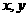 ,满足
,满足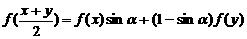 ,
,
求:(1) 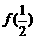 及
及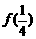 的值; (2)函数
的值; (2)函数 的单调递增区间;
的单调递增区间;
(3) 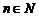 时,
时,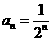 ,求
,求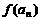 ,并猜测
,并猜测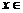
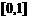 时,
时,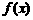 的表达式
的表达式
06届南通市小海中学期中考试试卷 2005-11
13已知 |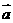 |=1,|
|=1,|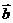 |=
|=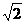 ,若
,若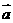 //
//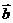 且
且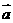 与
与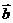 同向,则
同向,则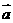 ·
·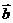 ____________.
____________.
14已知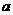 为实数,
为实数,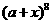 展开式中
展开式中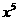 的系数为
的系数为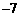 ,则
,则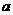 =____________.
=____________.
15 在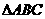 中,
中,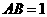
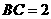 ,
,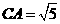 ,则
,则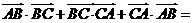 _______.
_______.
16在数列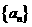 中,
中,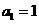 ,
,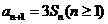 ,则数列{an}的通项公式
,则数列{an}的通项公式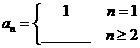
06届南通市小海中学期中考试试卷 2005-11
数学试卷
第Ⅱ卷(非选择题,共90分)
1设全集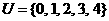 ,集合
,集合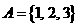 ,
,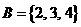 ,则
,则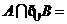 ( )
( )
A 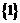 B
B 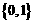 C
C 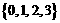 D
D
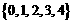
2已知数列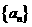 的前
的前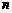 项和为
项和为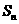 ,且
,且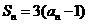 则
则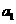 等于 ( )
等于 ( )
A 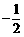 B
B 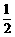 C
C 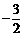 D
D
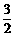
3不等式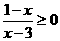 的解集是 ( )
的解集是 ( )
A 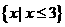 B
B
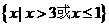 C
C 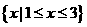 D
D 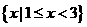
4给定两个向量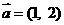 ,
,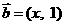 ,若
,若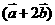 与
与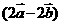 平行,则x的值等于( )
平行,则x的值等于( )
A 1 B 2 C 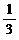 D
D 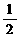
5对于数列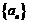 ,“对任意
,“对任意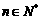 ,点
,点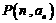 都在直线
都在直线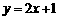 上”是“
上”是“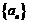 为等差数列”的
( )
为等差数列”的
( )
A 充分不必要条件 B 必要不充分条件
C 充要条件 D 既不充分也不必要条件
6已知抛物线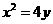 ,则它的焦点坐标是
( )
,则它的焦点坐标是
( )
A 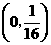 B
B
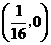 C
C 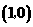 D
D
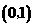
7若y = x + b与y = ax + 3互为反函数,则 a + b = ( ) A -2 B 2 C 4 D -10
8若要得到函数y=sin(2x-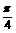 )的图像,可以把函数y=sin2x的图像
( )
)的图像,可以把函数y=sin2x的图像
( )
A
向右平移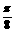 个单位
B 向左平移
个单位
B 向左平移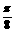 个单位
个单位
C 向左平移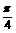 个单位
D 向右平移
个单位
D 向右平移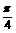 个单位
个单位
9函数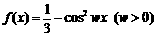 的周期与函数
的周期与函数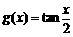 的周期相等,则
的周期相等,则 等于 ( )
等于 ( )
A 2 B 1 C 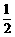 D
D 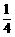
10函数f(q ) = 的最大值和最小值分别是 ( ) A 最大值 和最小值0 B 最大值不存在和最小值
C 最大值 -和最小值0 D 最大值不存在和最小值-
11函数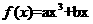 在x=
在x=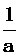 处有极值,则
处有极值,则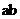 的值为 (
)
的值为 (
)
A 3 B -3 C 0 D 1
12已知数列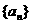 前n项和为
前n项和为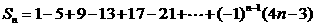 ,
,
则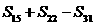 的值是
( )
的值是
( )
A 13 B -76 C 46 D 76
选择题答案填在下面表格内:
案填在题中横线上。
(9)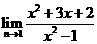 的值等于
的值等于 .
(10)在
.
(10)在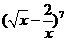 的展开式中,
的展开式中, 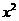 的系数是
的系数是 .(用数字作答)
.(用数字作答)
(11)若三点 A(2,2),B(a,0),C(0,b)(0 ,b)(ab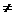 0)共线,则,
0)共线,则,
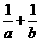 的值等于
的值等于
(12)在△ABC 中,若 C B A sin A: sinB: sinC =5:7:8. 则∠B 的大小是
 (13)已知点 P(x,y)的坐标满足条件
(13)已知点 P(x,y)的坐标满足条件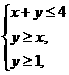 点O为坐标原点,那么|PO |的最小值
点O为坐标原点,那么|PO |的最小值
等于 ,最大值等于
,最大值等于 .
.
(14)已知A、B、C三点在球心为 O,半径为R 的球面上,AC⊥BC,且 AB=R,那么 A、B 两点间的球面距离为 球心到平面 ABC 的距离为
球心到平面 ABC 的距离为 .
.
. 三、解答题:本大题共 6 小题,共 80 分。解答应写出文字说明,证明过程或演算步骤。
(15)(本小题共 12 分)
已知函数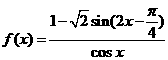 .
.
(Ⅰ)求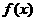 的定义域;
的定义域;
(Ⅱ)设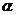 的第四象限的角,且
的第四象限的角,且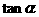
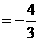 ,求
,求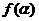 的值
的值
(16)(本小题共 13 分)
已知函数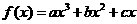 在点
在点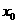 处取得极大值5,其导函数
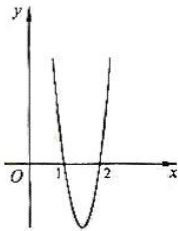
处取得极大值5,其导函数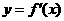
的图象经过点(1,0),(2,0),如图所示,求:
(Ⅰ)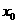 的值; (Ⅱ)a,b,c 的值.
的值; (Ⅱ)a,b,c 的值.
(17)(本小题共 14 分)
如图,在底面为平行四边形的四棱锥 P-ABCD 中,AB⊥AC,PA⊥平面 ABCD,且
PA=PB,点 E 是 PD 的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB//平面 AEC; 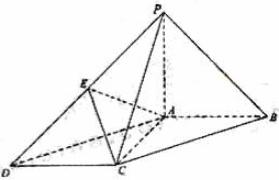
(Ⅲ)求二面角 E-AC-B 的大小.
(18)(本小题共 13 分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是 a,b,c,且三门课程考
试是否及格相互之间没有影响. 求:
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
(19)(本小题共 14 分)
已知点 M(-2,0),N(2,0),动点 P满足条件|PM |-|PN |=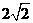 ,记动点 P的轨
,记动点 P的轨
迹为 W.
(Ⅰ)求 W 的方程;
(Ⅱ)若 A,B 是W上的不同两点,O 是坐标原点,求
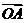 、
、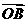 的最小值.
的最小值.
(20)(本小题共 14 分)
在数列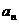 中,若 a1,a2 是正整数,且
中,若 a1,a2 是正整数,且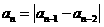 ,
,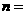 3,4,5,…,则称
3,4,5,…,则称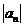
为“绝对差数列”.
(Ⅰ)举出一个前五项不为零的“绝对差数列”(只要求写出前十项);
(Ⅱ)若“绝对差数列”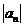 中,
中,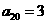 ,
,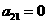 ,数列
,数列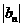 满足
满足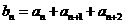
n=1,2,3,…,分虽判断当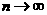 时,
时, 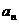 与
与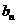 的极限是否存在,如果存在,求出其极
的极限是否存在,如果存在,求出其极
限值;
(Ⅲ)证明:任何“绝对差数列”中总含有无穷多个为零的项.
(1)在复平面内,复数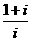 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
(2)若 a 与 b-c 都是非零向量,则“a·b=a·c”是“a⊥(b-c)”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(3)在 1,2,3,4,5 这五个数字组成的没有重复数字的三位数中,各位数字之和为
(A)36 个 (B)24 个
(C)18 个 (D)6 个
(4)平面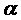 的斜线 AB 交
的斜线 AB 交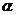 于点 B,过定点 A 的动直线
于点 B,过定点 A 的动直线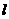 与 AB 垂直,且交
与 AB 垂直,且交
于点 C,则动 点 C 的轨迹是
(A)一条直线 (B)一个圆
(C)一个椭圆 (D)双曲线的一支
(5)已知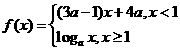 是
是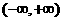 上的增函数,那么 a 的取值范
上的增函数,那么 a 的取值范
围是
(A)(0,1) (B)(0,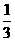 )
)
(C)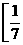 ,
,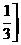 (D)
(D)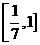
(6)在下列四个函数中,满足性质:“对于区间(1,2)上的任意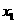 ,
,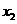 (
(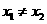 ).
).
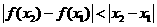 恒成立”的只有
恒成立”的只有
(A)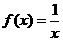 (B)
(B)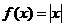
(C)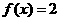 (D)
(D)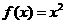
(7)设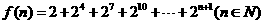 ,则
,则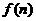 等于
等于
(A)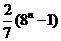 (B)
(B)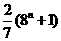
(C)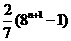 (D)
(D)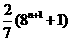
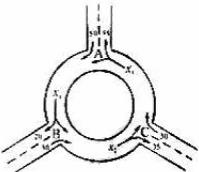
(8)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、
C 的机动车辆数如图所示,图中
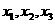 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段 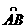 ,
,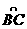
 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A) 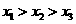
 (B)
(B) 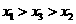
(C)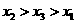
(D)
(D)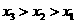
绝密★启用前
2006 年普通高等学校招生全国统一考试
数 学(文史类) (北京卷)
第 II 卷(共 110 分)
21、本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分。
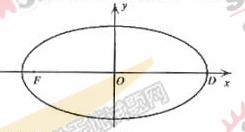 已知在平面直角坐标系
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为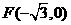 ,右顶点为
,右顶点为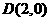 ,设点
,设点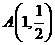 .
.
(1)求该椭圆的标准方程;
(2)若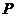 是椭圆上的动点,求线段
是椭圆上的动点,求线段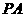 中点
中点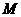 的轨迹方程;
的轨迹方程;
(3)过原点 的直线交椭圆于点
的直线交椭圆于点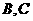 ,求
,求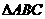 面积的最大值。
面积的最大值。
22(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分。
已知函数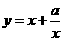 有如下性质:如果常数
有如下性质:如果常数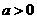 ,那么该函数在
,那么该函数在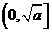 上是减函数,在
上是减函数,在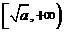 上是增函数。
上是增函数。
(1)如果函数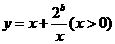 在
在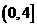 上是减函数,在
上是减函数,在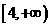 上是增函数,求
上是增函数,求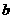 的值。
的值。
(2)设常数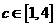 ,求函数
,求函数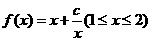 的最大值和最小值;
的最大值和最小值;
(3)当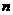 是正整数时,研究函数
是正整数时,研究函数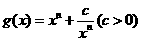 的单调性,并说明理由。
的单调性,并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com