
题目列表(包括答案和解析)
23、(本小题满分14分)已知正项数列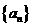 满足
满足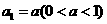 ,且
,且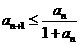 ,求证:(1)
,求证:(1)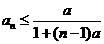 ; (2)
; (2)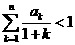 。
。
22、(本小题满分14分)已知椭圆C: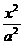 +
+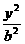 =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设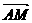 =λ
=λ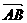 .
.
(Ⅰ)证明:λ=1-e2; (Ⅱ)确定λ的值,使得△PF1F2是等腰三角形.
21、(本小题满分14分)对定义域分别是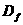 、
、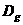 的函数
的函数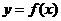 、
、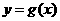 ,规定:函数
,规定:函数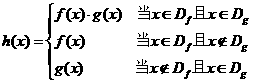
(1)若函数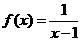 ,
,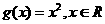 ,写出函数
,写出函数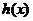 的解析式;
的解析式;
(2)求问题(1)中函数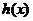 的值域。
的值域。
20、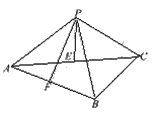 (本小题满分13分)已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(本小题满分13分)已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P-AB-C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的
球面上,求△ABC的边长.
19、(本小题满分12分)已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
18、有两个相同的直三棱柱,高为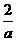 ,底面三角形的三边长分别为3a、4a、5a(a>0)。用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是
.
,底面三角形的三边长分别为3a、4a、5a(a>0)。用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是
.
17、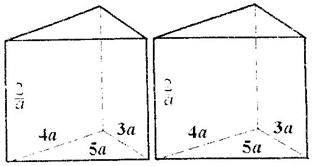 函数f(x)=sinx+2
函数f(x)=sinx+2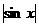 ,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是
.
,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围是
.
16、直角坐标平面xoy中,若定点A(1,2)与动点P(x,y)满足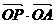 =4。则点P的轨
=4。则点P的轨
迹方程是 .
15、某班有50名学生,其中 15人选修A课程,另外35人选修B课程.从班级中任选两名学生,他们是选修不同课程的学生的慨率是 .(结果用分数表示)
14、设函数f(x)的图象关于点(1,2)对称,且存在反函数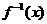 ,f (4)=0,则
,f (4)=0,则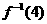 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com