
题目列表(包括答案和解析)
2、已知实数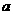 、
、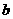 、
、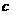 、
、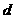 ,满足
,满足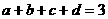 ,
,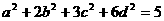 ,则
,则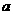 的最小值与最大值和为 ( )
的最小值与最大值和为 ( )
A.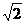 +1 B.
+1 B.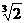 +1 C.
+1 C.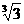 +
+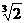 D.3
D.3
1、已知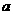 、
、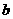 、
、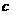
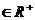 ,且
,且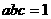 ,则
,则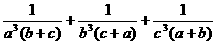 的最小值为( )
的最小值为( )
A.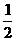 B.
B. 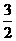 C.
C.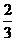 D.2
D.2
例9、设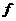 为(1,
为(1,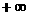 )→(1,
)→(1,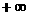 )的函数,且满足对任意
)的函数,且满足对任意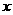 ,
,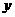 >1及
>1及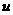 ,
,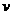 >0都成立着
>0都成立着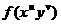 ≤
≤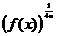 ·
·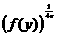 ,试确定所有这样的函数
,试确定所有这样的函数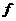 .
.
例10、试决定下式的最小值
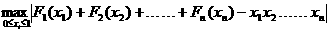 (对一切可能的实值函数0≤
(对一切可能的实值函数0≤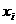 ≤1,
≤1,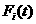 )(0≤
)(0≤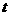 ≤1,1≤
≤1,1≤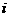 ≤n).
≤n).
例7、设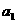 ,
,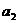 ,……
,……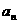 是正数,
是正数,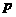 是自然数,求证:
是自然数,求证:
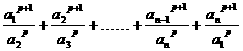 ≥
≥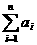
例8、设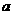 、
、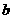 为正整数,
为正整数,
求证: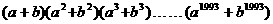 ≥
≥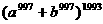
例5、设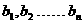
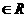 ,而
,而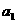 ≥
≥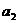 ≥……
≥……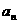 ≥0,又
≥0,又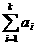 ≤
≤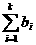 (
(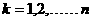 )
)
试证: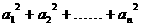 ≤
≤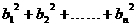
例6、证明:使对任何满足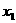 ≤
≤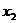 ≤……≤
≤……≤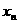 的实数, 不等式
的实数, 不等式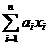 ≤
≤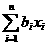 都成立的充分必要条件是
都成立的充分必要条件是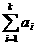 ≥
≥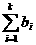 (
(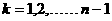 ),及
),及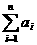 =
=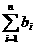
例1、已知0≤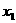 ≤
≤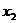 ≤……≤
≤……≤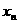 <1,
<1,
求证: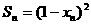 ·
·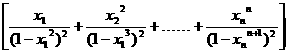 <1
<1
例2、已知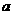 、
、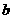 、
、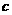 ∈
∈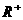 ,且满足
,且满足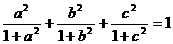 ,求证:
,求证: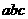 ≤
≤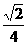
例3、设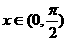 ,
,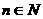 ,求证:
,求证: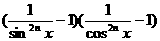 ≥
≥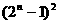
例4、设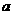 、
、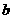 为正常数,
为正常数,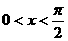 ,
,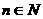 ,求证:
,求证: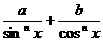 ≥
≥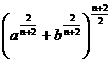
2、和式的变换
1、几个著名不等式
平均不等式:
柯西不等式:
排序不等式:
凸函数及琴生不等式:
赫尔德不等式:
切比雪夫不等式:
10.(选做题)某工厂有216名工人接受了生产1000台GH型高科技产品的总任务,已知每台GH型产品由4个G型装置和3个H型装置配套组成,每个工人每小时能加工6个G型装置或3个H型装置,现将工人分成两组,同时开始加工,每组分别加工一种装置,设加工G型装置的工人有x人,他们加工完G型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x)(单位:h,可不为整数)
(1) 写出g(x),h(x)的解析式;
(2) 比较g(x)与h(x)的大小,并写出这216名工人完成总任务的时间f(x)的解析式;
(3) 问:应怎样分组,才能使完成总任务的时间最少?
9.学校食堂定期从粮店以每吨1500元的价格购买大米,每次购进大米需支付运输费200元。食堂每天需要大米1吨,储存大米的费用为每吨每天1元,假设食堂每次均在用完大米的当天购买。
(1) 该食堂每多少天购买一次大米可使平均每天支付的总费用最少?
(2) 粮店提出价格优惠重要条件:一次购买量不少与40吨时,大米价格可享受九五折优惠(即原价的95%),问食堂可否接受此优惠条件?说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com