
题目列表(包括答案和解析)
7、巨幅壁画最高点离地面14m,最低点距地面2m,若从离地面1.5m处观赏此画,问离墙多远时视角最大。
6.已知,在等比数列{an}中,其首项a1>0,公比q>-1,且q≠1,前n项和为Sn;在数列{bn}
中bn=an+1-kan+2,前n项和为Tn。求证:(1)Sn>0;(2)若Tn>
kSn对一切正整数n成立,则k≤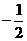 。
。
5.若不等式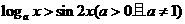 对于任意
对于任意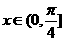 都成立,则a的取值
都成立,则a的取值
( )
A.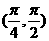 B.
B.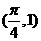 C.
C.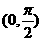 D.
D.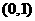
4.已知数列{an}的通项公式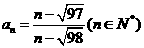 则数列的前30项中的最大值和最小值分别为 ( )
则数列的前30项中的最大值和最小值分别为 ( )
A.a1,a30 B. a1,a9 C.a10,a30 D. a10,a9
3.已知x,y为正整数,且x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则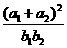 的取值范围是
( )
的取值范围是
( )
A.(0,4]
B.[4,+ ) C.(-
) C.(- ,0]
,0]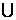 [4,+
[4,+ )
D.R
)
D.R
2.函数y= +
+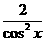 的最小值是
的最小值是
1.设实数x,y满足x2+(y-1)2=1,若对满足条件的x,y。x+y+c 0恒成立,则c的取值范围是
( )
0恒成立,则c的取值范围是
( )
A[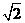 -1,+
-1,+ ) B (-
) B (- ,
,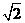 -1] C [
-1] C [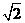 +1,+
+1,+ ) D (-
) D (- ,
,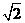 -1]
-1]
10.(选做题)设x=logst+logts,y=logs4t+logt4s+m(logs2t+logt2s),其中,s>1,t>1,m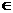 R
R
(1)将y表示成x的函数y=f(x),并求f(x)的定义域;
(2)若关于x的方程f(x)=0有且仅有一个实数根,求m的取值范围;
(3)若f(x)>0恒成立,求m的取值范围。
高三数学教学案 第六章 不等式
班级 学号 姓名
第十课时 不等式的综合运用(2)
目标要求
能够利用不等式解决与三角、数列有关的问题。进一步掌握不等式的性质与解法,提高综合解题能力。
例题讲解
例1.设x、y∈R,x2+y2=1,则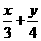 的最大值为
。
的最大值为
。
例2.已知{an}为等差数列,{bn}为等差数列,其公比q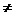 1,且bi>0(i=1,2,3,…,n)若a1=b1,a11=b11则 ( )
1,且bi>0(i=1,2,3,…,n)若a1=b1,a11=b11则 ( )
A.a6=b6 B.a6>b6 C.a6<b6 D.a6>b6 或 a6<b6
例3.在△ABC中,角A、B、C的对边分别为a,b,c,其中c为最大边,并且sin2A+sin2B=1。
(1)判断△ABC的形状,并给出证明;
(2)当c=2时,求△ABC面积的最大值。
例4.已知a>0且a≠1,数列{an}是首项为a,公比也为a的等比数列,令bn=anlgan(n∈N+)问是否存在实数a,对任意正整数n,数列{bn}中的每一项总小于它后面的项?若存在,求出相应的a的范围;若不存在,说明理由。
例5.设数列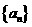 满足a1=2,an+1=an+
满足a1=2,an+1=an+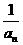 (n=1,2,3,……)
(n=1,2,3,……)
(1)证明:an>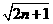 对一切正整数n成立;
对一切正整数n成立;
(2)令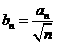 (n=1,2,3,……),判断bn与bn+1的大小。并说明理由。
(n=1,2,3,……),判断bn与bn+1的大小。并说明理由。
班级 学号 姓名
课后作业
9.已知二次函数f(x)=ax2+bx+1(a,b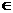 R,a>0),设方程f(x)=x的两个实数根分别为x1,x2,
R,a>0),设方程f(x)=x的两个实数根分别为x1,x2,
(1)如果x1<2<x2<4,设函数f(x)的对称轴为x=x0,求证:x0>-1;
(2)如果|x1|<2,|x1-x2|=2,求证:b<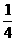 或b>
或b>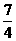 。
。
8.若对一切实数x,不等式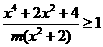 均成立,求实数m的取值范围。
均成立,求实数m的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com