
题目列表(包括答案和解析)
20.解:
设事件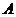 为“方程
为“方程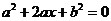 有实根”.
有实根”.
当 ,
,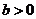 时,方程
时,方程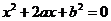 有实根的充要条件为
有实根的充要条件为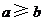 .
.
(Ⅰ)基本事件共12个:
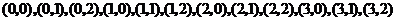 .其中第一个数表示
.其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值.
的取值.
事件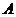 中包含9个基本事件,事件
中包含9个基本事件,事件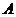 发生的概率为
发生的概率为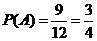 .
.
(Ⅱ)试验的全部结束所构成的区域为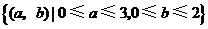 .
.
构成事件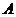 的区域为
的区域为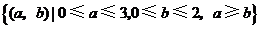 .
.
所以所求的概率为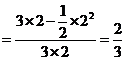 .
.
辽宁理
20.(本小题满分12分)
设有关于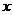 的一元二次方程
的一元二次方程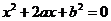 .
.
(Ⅰ)若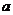 是从
是从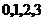 四个数中任取的一个数,
四个数中任取的一个数,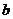 是从
是从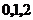 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若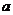 是从区间
是从区间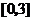 任取的一个数,
任取的一个数,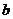 是从区间
是从区间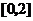 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
20.解:
每个点落入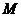 中的概率均为
中的概率均为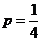 .
.
依题意知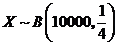 .
.
(Ⅰ)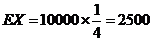 .
.
(Ⅱ)依题意所求概率为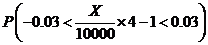 ,
,

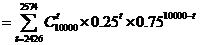
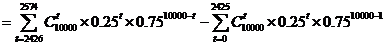
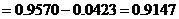 .
.
宁夏文
20.(本小题满分12分)
如图,面积为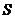 的正方形
的正方形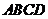 中有一个不规则的图形
中有一个不规则的图形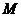 ,可按下面方法估计
,可按下面方法估计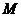 的面积:在正方形
的面积:在正方形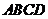 中随机投掷
中随机投掷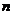 个点,若
个点,若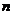 个点中有
个点中有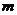 个点落入
个点落入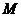 中,则
中,则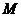 的面积的估计值为
的面积的估计值为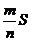 ,假设正方形
,假设正方形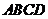 的边长为2,
的边长为2,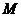 的面积为1,并向正方形
的面积为1,并向正方形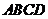 中随机投掷
中随机投掷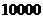 个点,以
个点,以 表示落入
表示落入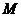 中的点的数目.
中的点的数目.
(I)求 的均值
的均值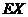 ;
;
(II)求用以上方法估计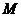 的面积时,
的面积时,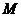 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间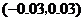 内的概率.
内的概率.
附表:
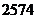
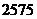
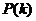
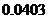
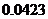
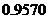
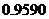
11.甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表
|
甲的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
5 |
5 |
5 |
5 |
|
乙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
6 |
4 |
4 |
6 |
|
丙的成绩 |
||||
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
4 |
6 |
6 |
4 |
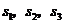 分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )
 A.
A.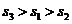 B.
B.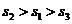
C.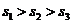 D.
D.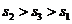
18.解:
(Ⅰ)记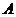 表示事件:“
表示事件:“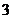 位顾客中至少
位顾客中至少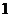 位采用一次性付款”,则
位采用一次性付款”,则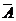 表示事件:“
表示事件:“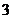 位顾客中无人采用一次性付款”.
位顾客中无人采用一次性付款”.
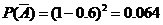 ,
,
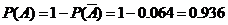 .
.
(Ⅱ)记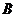 表示事件:“
表示事件:“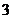 位顾客每人购买
位顾客每人购买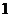 件该商品,商场获得利润不超过
件该商品,商场获得利润不超过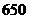 元”.
元”.
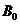 表示事件:“购买该商品的
表示事件:“购买该商品的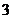 位顾客中无人采用分期付款”.
位顾客中无人采用分期付款”.
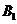 表示事件:“购买该商品的
表示事件:“购买该商品的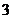 位顾客中恰有
位顾客中恰有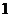 位采用分期付款”.
位采用分期付款”.
则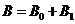 .
.
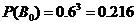 ,
,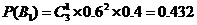 .
.
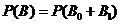
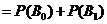
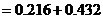
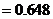 .
.
全国I理
(18)(本小题满分12分)
某商场经销某商品,根据以往资料统计,顾客采用的付款期数 的分布列为
的分布列为
 |
1 |
2 |
3 |
4 |
5 |
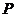 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.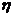 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件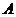 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率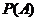 ;
;
(Ⅱ)求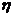 的分布列及期望
的分布列及期望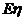 .
.
(18)解:
(Ⅰ)由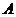 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
知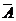 表示事件“购买该商品的3位顾客中无人采用1期付款”
表示事件“购买该商品的3位顾客中无人采用1期付款”
 ,
,
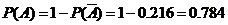 .
.
(Ⅱ)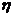 的可能取值为
的可能取值为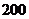 元,
元,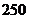 元,
元,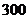 元.
元.
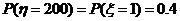 ,
,
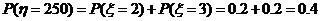 ,
,
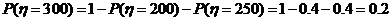 .
.
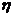 的分布列为
的分布列为
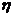
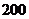
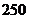
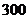
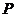
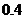
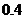
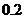
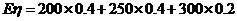
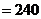 (元).
(元).
宁夏理
19.(1)记 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,
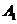 表示事件“取出的2件产品中恰有1件二等品”.
表示事件“取出的2件产品中恰有1件二等品”.
则 互斥,且
互斥,且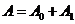 ,故
,故
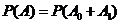
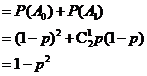
于是 .
.
解得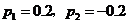 (舍去).
(舍去).
(2)记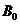 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,
则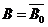 .
.
若该批产品共100件,由(1)知其中二等品有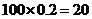 件,故
件,故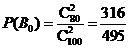 .
.
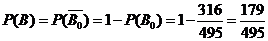
全国I文
(13)从某自动包装机包装的食盐中,随机抽取 袋,测得各袋的质量分别为(单位:
袋,测得各袋的质量分别为(单位: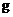 ):
):
|
492 |
496 |
494 |
495 |
498 |
497 |
501 |
502 |
504 |
496 |
|
497 |
503 |
506 |
508 |
507 |
492 |
496 |
500 |
501 |
499 |
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5g-501.5g之间的概率约为_____.0.25
(18)(本小题满分12分)
某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6,经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.
(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;
(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率.
19.(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件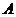 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率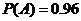 .
.
(1)求从该批产品中任取1件是二等品的概率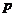 ;
;
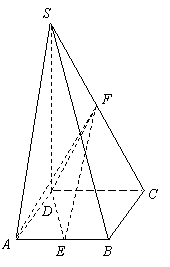 (2)若该批产品共100件,从中任意抽取2件,求事件
(2)若该批产品共100件,从中任意抽取2件,求事件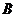 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率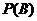 .
.
13.一个总体含有100个个体,以简单随机抽样方式从该总体中抽取一个容量为5的样本,则指定的某个个体被抽到的概率为 .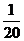
18.解:(1)记 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,
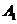 表示事件“取出的2件产品中恰有1件二等品”.
表示事件“取出的2件产品中恰有1件二等品”.
则 互斥,且
互斥,且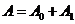 ,故
,故
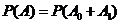
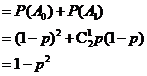
于是 .
.
解得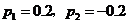 (舍去).
(舍去).
(2) 的可能取值为
的可能取值为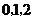 .
.
若该批产品共100件,由(1)知其二等品有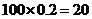 件,故
件,故
 .
.
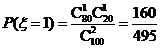 .
.
 .
.
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
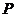 |
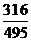 |
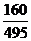 |
 |
全国II文
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com