
题目列表(包括答案和解析)
4.函数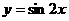 的图象按向量
的图象按向量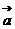 平移后,所得函数的解析式是
平移后,所得函数的解析式是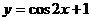 ,则
,则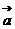 =________(答:
=________(答: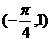 )
)
3.已知平面上三点A、B、C满足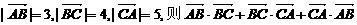 的值等于 ( C )
的值等于 ( C )
A.25 B.24 C.-25 D.-24
2.“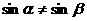 ”是“
”是“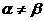 ”的 条件。(答:充分非必要条件)
”的 条件。(答:充分非必要条件)
1.在△ABC中,a、b、c分别为角A、B、C的对边,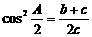 ,则△ABC的形状为( B )
,则△ABC的形状为( B )
A.正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
22.解: (Ⅰ)由于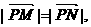 则P为MN的中心,……1分,
则P为MN的中心,……1分,
设N(x,y),则M(-x,0),P(0,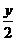 ),……(2分),由
),……(2分),由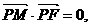 得
得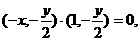
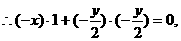
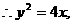 所以点N的轨迹方程为
所以点N的轨迹方程为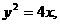 ……5分
……5分
(Ⅱ)设直线l的方程是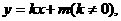 与
与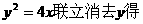 :
:
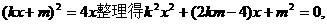 ……………………6分
……………………6分
设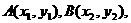 则:
则: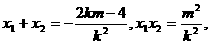
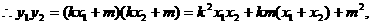
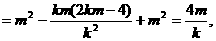 ……………………7分
……………………7分
由
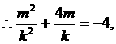 即
即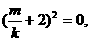
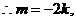 …………9分
…………9分
由于直线与N的轨迹交于不同的两点,则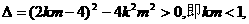
把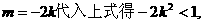
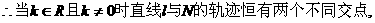 ………………10分
………………10分
而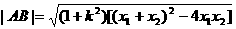
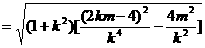
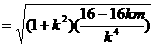
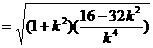
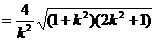 …11分
…11分
又因为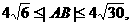
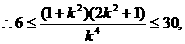
解得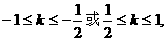
综上可知k的取值范围是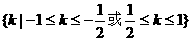 .…14分
.…14分
21.解:(1)由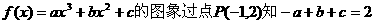 ①……1分
①……1分
又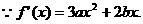
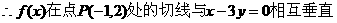 ,
, 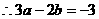 ②…3分
②…3分
又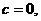 ①、②联立得:
①、②联立得: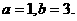
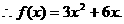 ……4分
……4分
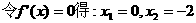
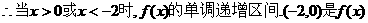 的单调递减区间.…6分
的单调递减区间.…6分
(2)令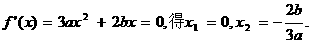
又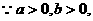
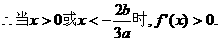
即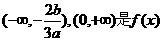 单调递增区间.
单调递增区间.
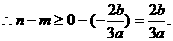 …………………………8分
…………………………8分
由(1)知: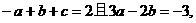
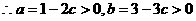
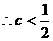 ………10分
………10分
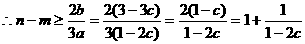 ……11分
……11分
由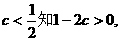
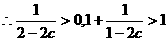
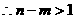 ……………12分
……………12分
另解:由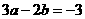 得:
得: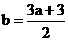
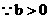

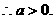 …10分
…10分 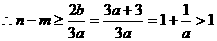 ……12分
……12分
注:若用b表示a,酌情给分.
20.
解::(I)基本事件总数为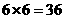 ,
,
若使方程有实根,则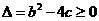 ,即
,即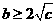 。
。
当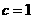 时,
时,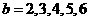 ;
;
当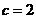 时,
时,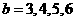 ;
;
当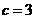 时,
时,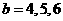 ;
;
当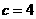 时,
时,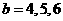 ;
;
当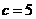 时,
时,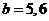 ;
;
当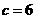 时,
时,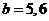 ,
,
目标事件个数为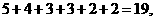
因此方程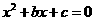 有实根的概率为
有实根的概率为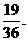
(II) 记“先后两次出现的点数中有5”为事件M,“方程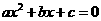 有实根” 为事件N,则
有实根” 为事件N,则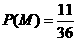 ,
,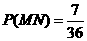 ,
,
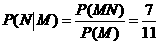 .
.
20.解:记AEFB表示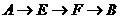 不堵车,其它类似.
不堵车,其它类似.
(1) P(AEFB)=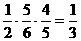 , P(ACDB)=
, P(ACDB)=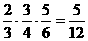 ,P(ACFB)=
,P(ACFB)=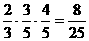 ,
,
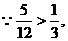
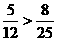 ,
,

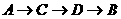 为最佳路线.
为最佳路线.
(2)设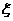 表示
表示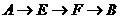 中堵车次数.则
中堵车次数.则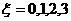
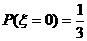 ,
,
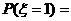
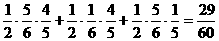 ,
,
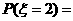
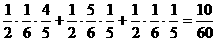 ,
,
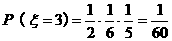 ,
,
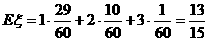 .
.
18.解: (Ⅰ)设二次函数为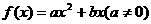 …………1分
…………1分
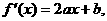
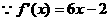
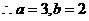
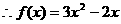 ……3分,又
……3分,又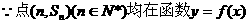 的图象上.
的图象上.
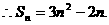 ………………………………4分
………………………………4分
当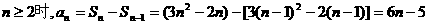 ……5分
……5分
当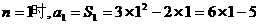 ,满足上式
,满足上式
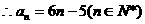 ………………………………6分
………………………………6分
(Ⅱ)由(Ⅰ)得: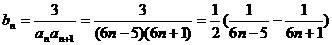 ………8分
………8分
故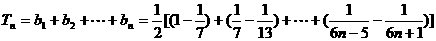
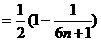 ……………………10分
……………………10分
要使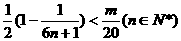 都成立 必须且只须
都成立 必须且只须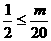
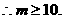
 …………12分
…………12分
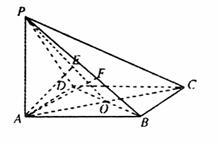 19.解法一:
19.解法一:
(Ⅰ)证明:设AC与BD交于O,连结PO

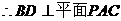 ……………………(3分)
……………………(3分)
又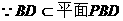
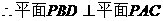 ……………………(4分)
……………………(4分)
(Ⅱ)作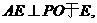
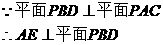
所以AE为点A到平面PBD的距离.…………(6分)
在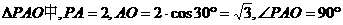
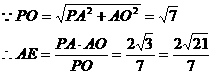 ,所以A点到平面PBD的距离为
,所以A点到平面PBD的距离为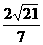 …8分
…8分
(Ⅲ)作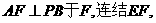
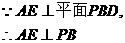
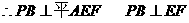
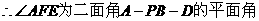 …10分
…10分
在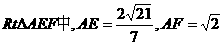 ,
,
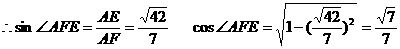
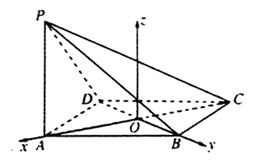 所以二面角A-PB-D的余弦值为
所以二面角A-PB-D的余弦值为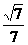 …………………12分
…………………12分
解法二:(Ⅰ)设AC与BD交于O点
以OA、OB所在直线分别x轴,y轴.
以过O且垂直平面ABCD的直线为z轴,建立
如图的空间直角坐标系,则
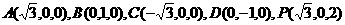
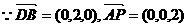 …………………………2分
…………………………2分
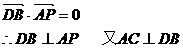
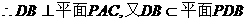
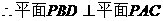 ……(4分)
……(4分)
(Ⅱ)设平面PDB的法向量为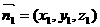 ,
,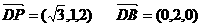
由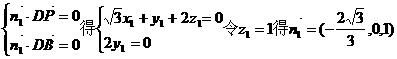 …………6分
…………6分
 =
=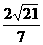 …………8分
…………8分
(Ⅲ)设平面ABP的法向量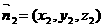
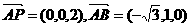
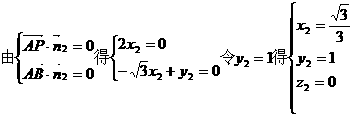
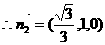 …10分
…10分
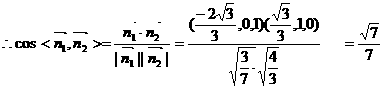 …………11分
…………11分
所以二面角A-PB-D的余弦值为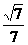 …………12分
…………12分
17.解: (Ⅰ)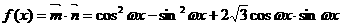
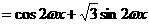
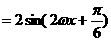 ………………3分
………………3分
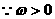
 ……………4分
……………4分
由题意可知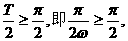
解得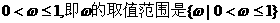 ……………………5分
……………………5分
(Ⅱ)由(Ⅰ)可知 的最大值为1,
的最大值为1,
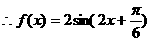
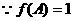
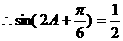 ……………6分
……………6分
而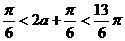
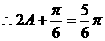
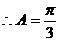 ………………8分
………………8分
由余弦定理知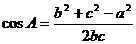
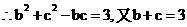 …10
…10
联立解得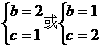 ………11分
………11分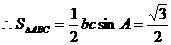 ……12分
……12分
(或用配方法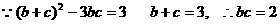
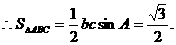 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com