
题目列表(包括答案和解析)
18.(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
18.(本小题满分13分,其中(Ⅰ)小问4分,(Ⅱ)小问9分)
某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆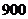 元的保险金,对在一年内发生此种事故的每辆汽车,单位可获
元的保险金,对在一年内发生此种事故的每辆汽车,单位可获 元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为
元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为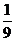 ,
,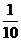 ,
,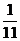 ,且各车是否发生事故相互独立,求一年内该单位在此保险中:
,且各车是否发生事故相互独立,求一年内该单位在此保险中:
(Ⅰ)获赔的概率;
(Ⅱ)获赔金额 的分布列与期望.
的分布列与期望.
(18)(本小题13分)
解:设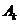 表示第
表示第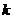 辆车在一年内发生此种事故,
辆车在一年内发生此种事故,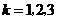 .由题意知
.由题意知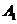 ,
,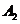 ,
,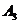 独立,
独立,
且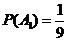 ,
,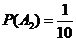 ,
,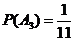 .
.
(Ⅰ)该单位一年内获赔的概率为
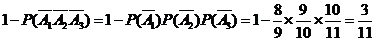 .
.
(Ⅱ) 的所有可能值为
的所有可能值为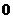 ,
, ,
,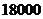 ,
, .
.
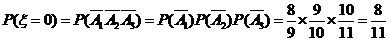 ,
,
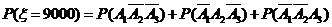
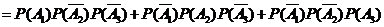
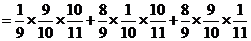
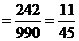 ,
,
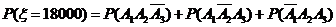
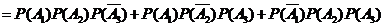
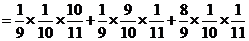
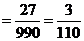 ,
,
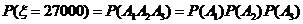
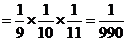 .
.
综上知, 的分布列为
的分布列为


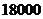
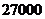
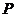
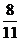
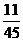

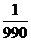
求 的期望有两种解法:
的期望有两种解法:
解法一:由 的分布列得
的分布列得
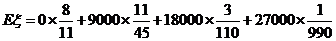
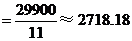 (元).
(元).
解法二:设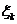 表示第
表示第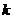 辆车一年内的获赔金额,
辆车一年内的获赔金额,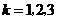 ,
,
则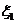 有分布列
有分布列
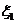
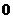

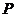
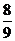
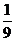
故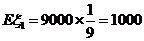 .
.
同理得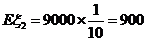 ,
,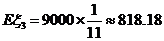 .
.
综上有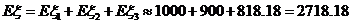 (元).
(元).
四川理
(12)已知一组抛物线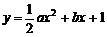 ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是
(A)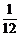 (B)
(B)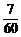 (C)
(C) (D)
(D)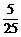
(18)(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数 的分布列及期望
的分布列及期望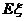 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
(18)本题考察相互独立事件、互斥事件等的概率计算,考察随机事件的分布列,数学期望等,考察运用所学知识与方法解决实际问题的能力。
解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有
(Ⅱ) 可能的取值为
可能的取值为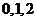
 ,
,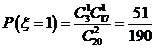 ,
,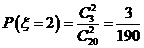

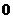
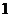
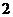
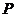

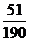
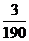
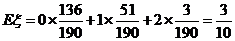
记“商家任取2件产品检验,都合格”为事件B,则商家拒收这批产品的概率
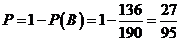
所以商家拒收这批产品的概率为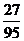
四川文
(3)某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,
149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是
(A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
天津理
※设L1、L2是两条异面直线,其公垂向量为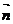 ,又C、D分别是L1、L2上任意一点,则
,又C、D分别是L1、L2上任意一点,则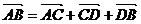
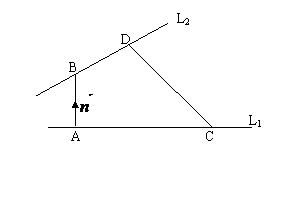
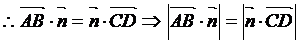
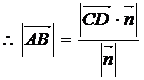
则L1、L2间的距离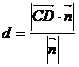
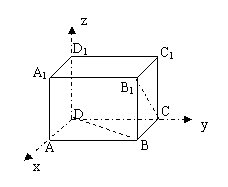 [例5]已知正方体ABCD-A1B1C1D1的棱长为
[例5]已知正方体ABCD-A1B1C1D1的棱长为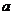 ,求异面直线BD与B1C的距离。
,求异面直线BD与B1C的距离。
解:如图,建立空间直角坐标系,则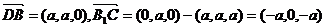
设DB与B1C的公垂向量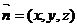
|
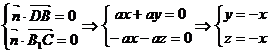
令x=-1,则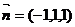 又
又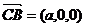 ,
,
所以异面直线BD与B1C的距离为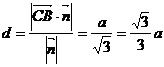 .
.
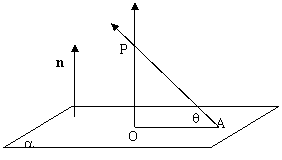
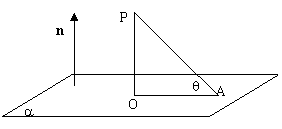 ※如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂线PO,记PA和平面a所成的角为q,则点P到平面的距离为
※如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂线PO,记PA和平面a所成的角为q,则点P到平面的距离为
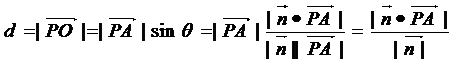
[例4]设A(2,3,1),B(4,1,2),C(6,3,7),D(-5,-4,8),
求D到平面ABC的距离。
解:设平面ABC的法向量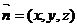
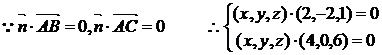
即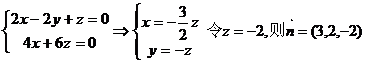
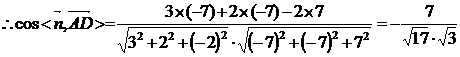
∴点D到平面ABC的距离为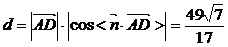
 ※如图在二面角
※如图在二面角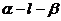 中
中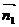 和
和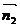 分别为
分别为
平面a和b的法向量若二面角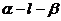 ,记二面角
,记二面角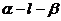 的大小为q。
的大小为q。
(ⅰ)若该二面角为锐二面角,则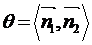 或
或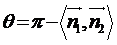 (依据两平面法向量的方向而定),但总有
(依据两平面法向量的方向而定),但总有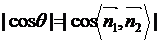 =
=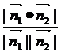 ,所以此时
,所以此时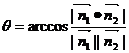 。
。
 (ⅱ)若二面角
(ⅱ)若二面角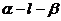 为钝二面角,
为钝二面角,
则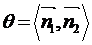 或
或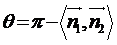
(依据两平面法向量的方向而定),
但总有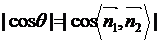 =
=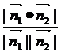
所以此时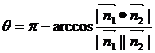
[例3]已知三棱锥P-ABCD中PA⊥面ABCD,底面ABCD为菱形,
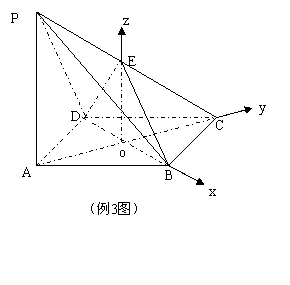 ∠BAD=600,AB=2,PA=4,E为PC的中点。
∠BAD=600,AB=2,PA=4,E为PC的中点。
(1)求证:平面BDE⊥平面ABCD
(2)求B-DE-C的大小
证明:(1)易证(略)
(2)设AC∩BD=O,连结OE,
以O为原点建立空间直角坐标系(如图)
由(1)得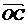 为平面EBD的法量,
为平面EBD的法量,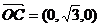 .
.
设平面CDE的法向量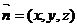
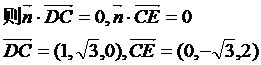
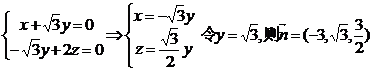
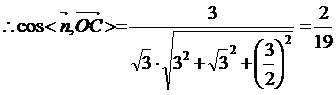 , 所以B-DE-C为
, 所以B-DE-C为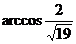 。
。
※直线与平面平行是直线与平面的法向量垂直问题,只取和直线平行的向量,验证该向量和平面的法向量的内积是否为零即可。
[例2]如图,四棱锥P-ABCD中PA⊥平面ABCD,PB与底面所成的角为450,底面ABCD为直角梯形,∠ABC=∠BAD=900,PA=BC=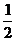 AD=
AD=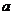
(1)求证:平面PAC⊥平面PCD(略)
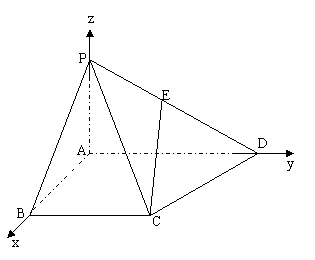 (2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置;若不存在,请说明理由。
(2)在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置;若不存在,请说明理由。
解:分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系(如图)
则P(0,0,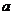 ),C(
),C(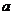 ,
,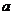 ,0),D(0,2
,0),D(0,2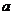 ,0)
,0)
设在棱PD上存在点E坐标为(0,y,z),
则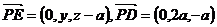
|
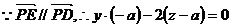
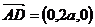 是平面PAB的法向量,又
是平面PAB的法向量,又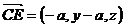
由CE//面PAB,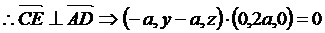
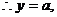 代入得
代入得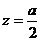
∴E是PD中点,
即存在点E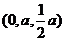 使得CE//面PAB。
使得CE//面PAB。
※直线与平面所成的角,是直线与平面的法向量所成的角(取锐角)的余角。
如图,已知PA为平面a的一条斜线,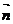 为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记q,易得
为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记q,易得
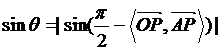

则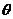 =
=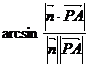
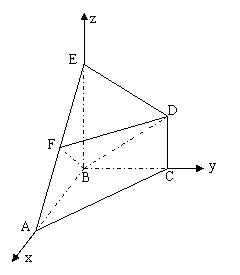 [例1]如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
[例1]如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
(1)证明:DF//平面ABC(略)
(2)求AB与平面BDF所成角的大小。
|
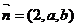
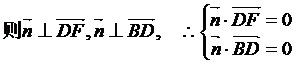 ,而
,而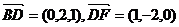
则得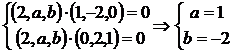 所以
所以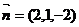
又设AB与平面BDF所成角为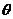 ,则法线
,则法线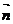 与
与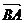 所成的角为
所成的角为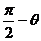

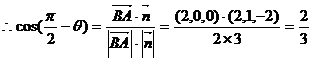
即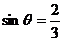 ,故AB与平面BDF所成的角为
,故AB与平面BDF所成的角为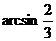
用法向量求解,不用作出AB与平面BDF所成的角,从而避开了作图的难度。
要证两平面相互垂直,只需找出这两个平面的两个法向量,证明这两个法向量相互垂直。
例9、
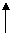 如右图,△ABC是一个正三角形,EC⊥平面ABC,
如右图,△ABC是一个正三角形,EC⊥平面ABC,


 BD∥CE,且CE=CA=2BD,M是EA的中点。
E
BD∥CE,且CE=CA=2BD,M是EA的中点。
E


 求证:(1)DE=DA;
M
D
求证:(1)DE=DA;
M
D




 (2)平面BDM⊥平面ECA;
C
B
(2)平面BDM⊥平面ECA;
C
B
(3)平面DEA⊥平面ECA; A
分析(3):建立如图所示右手直角坐标系
,不妨设CA=2,则CE=2,BD=1,C(0,0,0),A(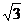 ,1,0),B(0,2,0),E(0,0,2),D(0,2,1),
,1,0),B(0,2,0),E(0,0,2),D(0,2,1),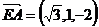 ,
,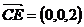 ,
,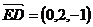 , 分别假设面CEA与面DEA的法向量是
, 分别假设面CEA与面DEA的法向量是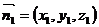 、
、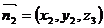 ,所以得
,所以得
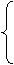

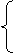
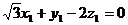
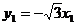
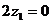
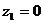
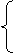
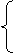
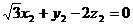
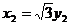
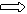
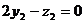

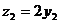
不妨取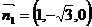 、
、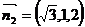 ,从而计算得
,从而计算得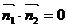 ,所以两个法向量相互垂直,两个平就相互垂直。
,所以两个法向量相互垂直,两个平就相互垂直。
事实证明,法向量在求角、距离以及证明平行垂直中都有非常广泛的应用,它在中学数学中的出现,是对传统的立体几何知识一个很好的补充及加深。
如果有一向量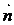 垂直于平面α,则向量
垂直于平面α,则向量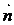 叫做平面α的法向量。要证两个平面平行,只需证这两个平面同时垂直于它们的法向量。
叫做平面α的法向量。要证两个平面平行,只需证这两个平面同时垂直于它们的法向量。
例8、已知正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面B1D1C
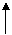 分析:作如图所示右手直角坐标系,
D
C
分析:作如图所示右手直角坐标系,
D
C








 则各点坐标是A1(1,0,0),
A
B
则各点坐标是A1(1,0,0),
A
B



 D1(0,0,0),B1(1,1,0),
D1 C1
D1(0,0,0),B1(1,1,0),
D1 C1





 B(1,1,1),D(0,0,1),
A1
B1
B(1,1,1),D(0,0,1),
A1
B1
 C(0,1,1) ,则
C(0,1,1) ,则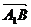 =(0,1,1),
=(0,1,1),
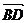 =(-1,-1,0),设平面A1BD有一法向量
=(-1,-1,0),设平面A1BD有一法向量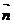 =(x,y,z),则
=(x,y,z),则
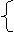
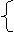 y+z
-x +-y =0
y+z
-x +-y =0
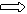 x=z
y=-z
x=z
y=-z
不妨取z=1,则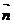 =(1,-1,1) ,又由
=(1,-1,1) ,又由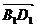 =(-1,-1,0),
=(-1,-1,0),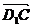 =(0,1,1),易知
=(0,1,1),易知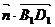 =
=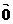 ,
, 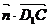 =
=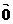 ,所以
,所以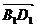 与
与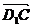 都与
都与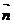 垂直,所以
垂直,所以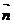 与平面B1D1C垂直,从而得到平面A1BD∥平面B1D1C
与平面B1D1C垂直,从而得到平面A1BD∥平面B1D1C
如图,要求直线a与平面α所成的角θ,先求这个平面α的法向量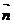 与直线a的夹角的余弦
与直线a的夹角的余弦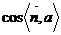 ,易知θ=
,易知θ=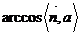 或者
或者
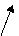 例7、如下图,已知正四面体ABCD的边长为2,E为AD的中点,求EC与平面BCD所成的角。
例7、如下图,已知正四面体ABCD的边长为2,E为AD的中点,求EC与平面BCD所成的角。



 分析:作AO⊥平面BCD,连结OD,并且
A
分析:作AO⊥平面BCD,连结OD,并且
A
 过O作OF∥BC交CD于F,建立如图所
E
过O作OF∥BC交CD于F,建立如图所
E

 示右手直角坐标系,则O(0,0,0),
B
O
D
示右手直角坐标系,则O(0,0,0),
B
O
D



 E(0,
E(0,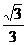 ,
,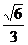 ),
), 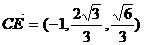 C
F
C
F
易取得平面BCD上的一个法向量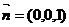 ,所以
,所以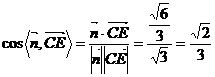 ,观察
,观察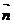 与
与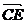 的方向,易知EC与平面BCD所成的角是
的方向,易知EC与平面BCD所成的角是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com