
题目列表(包括答案和解析)
13 已知
已知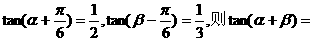

14 一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .
一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .
15 已知
已知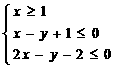 则
则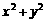 的最小值是
的最小值是

16.已知点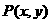 在圆
在圆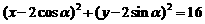 上运动,当角
上运动,当角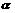 变化时,点
变化时,点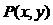 运动区域的面积为
.
运动区域的面积为
.
12.若关于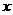 的方程
的方程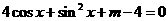 恒有实数解,则实数m的取值范围是( )
恒有实数解,则实数m的取值范围是( )
A. [0,8] B.[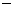 1,8] C.
[0,5]
D. [
1,8] C.
[0,5]
D. [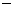 1,+∞)
1,+∞)
08届高考文科数学第一次联合考试试卷
第Ⅱ卷
1 已知集合M ={
已知集合M ={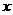 |
|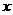 <
<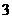 },N={x|
},N={x|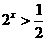 },则M ∩N等于
( )
},则M ∩N等于
( )
A Æ B
Æ B {x|-1<x<3} C
{x|-1<x<3} C {x|0<x<3} D
{x|0<x<3} D {x|1<x<3}
{x|1<x<3}
2 某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数应为
( )
某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数应为
( )
A 10 B
10 B 9 C
9 C 8 D
8 D 7
7
3 若函数
若函数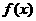 的反函数为
的反函数为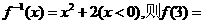 ( )
( )
A 1 B
1 B 11 C
11 C 1或-1 D
1或-1 D -1
-1
4 在等差数列
在等差数列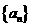 中,
中,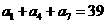 ,
,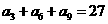 ,则数列
,则数列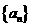 的前9项之和
的前9项之和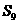 等于
( )
等于
( )
A.66 B.99 C.144 D.297
5 已知
已知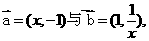 则不等式
则不等式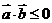 的解集为
( )
的解集为
( )
A
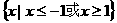 B
B
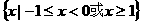
C
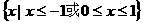 D
D
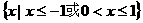
6 在
在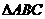 中,“
中,“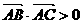 ”是“
”是“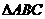 为锐角三角形”的( )
为锐角三角形”的( )
A 充分不必要条件 B
充分不必要条件 B 必要不充分条件
必要不充分条件
C 充要条件 D
充要条件 D 既非充分又非必要条件
既非充分又非必要条件
 7
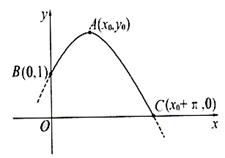
7 已知函数
已知函数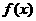 的部分图象如图所示,则
的部分图象如图所示,则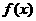 的解析式可能为
( )
的解析式可能为
( )
A
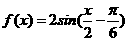
B
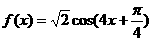
C
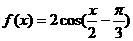
D
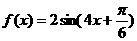
8.在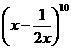 的展开式中,
的展开式中,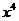 的系数为
( )
的系数为
( )
A
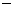 120
B
120
B 120
C
120
C
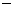 15
D
15
D 15
15
9 若直线
若直线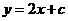 按向量
按向量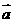 =(1,
=(1,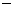 1)平移后与圆
1)平移后与圆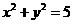 相切,则
相切,则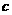 的值为( )
的值为( )
A. 8或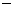 2 B.6或
2 B.6或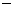 4 C.4或
4 C.4或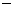 6 D.2或
6 D.2或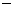 8
8
10 某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:
某次文艺汇演,要将A、B、C、D、E、F这六个不同节目编排成节目单,如下表:
|
序号 |
1 |
2 |
3 |
4 |
5 |
6 |
|
节目 |
|
|
|
|
|
|
如果A、B两个节目要相邻,且都不排在第3号位置,那么节目单上不同的排序方式
A 192种 B
192种 B 144种 C
144种 C 96种 D
96种 D 72种
72种
11 已知点
已知点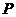 是以
是以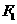 、
、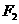 为焦点的椭圆
为焦点的椭圆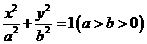 上的一点,若
上的一点,若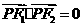 ,
,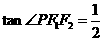 ,则此椭圆的离心率为
( )
,则此椭圆的离心率为
( )
A.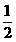 B.
B.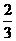 C.
C.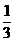 D.
D.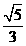
17 (本小题12分)
(本小题12分)
已知函数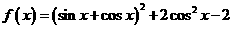

(I)求函数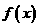 的最小正周期;
的最小正周期;
(II) 当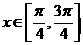 时,求函数
时,求函数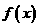 的最大值,最小值
的最大值,最小值
18 (本小题12分)
(本小题12分)
某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球获得二等奖;摸出两个红球获得一等奖.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.求
(1)甲、乙两人都没有中奖的概率;
(2)甲、乙两人中至少有一人获二等奖的概率.
19 (本小题满分12分)
(本小题满分12分)
如图,已知正三棱柱ABC- 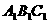 ,D是AC的中点,∠
,D是AC的中点,∠ DC = 60°
DC = 60°
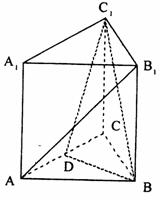 (Ⅰ)求证:A
(Ⅰ)求证:A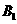 ∥平面B
∥平面B D;
D;
(Ⅱ)求二面角D-B -C的大小。
-C的大小。
20 (本小题12分)
(本小题12分)
已知函数f(x)=x3+ax2+bx+c在x=-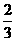 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值及函数f(x)的单调区间;
(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求c的取值范围.
21.(本小题12分)已知数列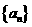 中的相邻两项
中的相邻两项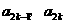 是关于
是关于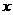 的方程
的方程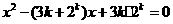 的两个根,且
的两个根,且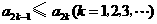 .
.
(I)求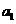 ,
,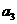 ,
,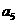 ,
,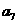 ;
;
(II)求数列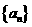 的前
的前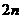 项的和
项的和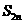 ;
;
(Ⅲ)求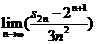
22 (本小题14分)
(本小题14分)
如图,在直角坐标系中,O为坐标原点,直线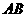 ⊥x轴与点C,
⊥x轴与点C, 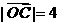 ,
,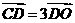 ,动点
,动点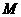 到直线
到直线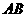 的距离是它到点D的距离的2倍
的距离是它到点D的距离的2倍
(I)求点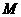 的轨迹方程;
的轨迹方程;
(II)设点K为点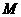 的轨迹与x轴正半轴的交点,直线
的轨迹与x轴正半轴的交点,直线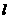 交点
交点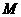 的轨迹于
的轨迹于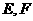 两点
两点
(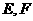 与点K均不重合),且满足
与点K均不重合),且满足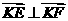
 求直线EF在X轴上的截距;
求直线EF在X轴上的截距;
(Ⅲ)在(II)的条件下,动点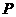 满足
满足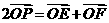 ,求直线
,求直线 的斜率的取值范围
的斜率的取值范围
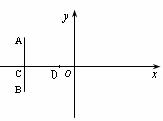
13 已知
已知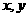 满足
满足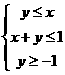 ,则
,则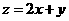 的最大值为
的最大值为

14 四面体
四面体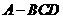 中,
中,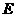 是
是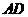 中点,
中点,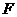 是
是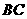 中点,
中点,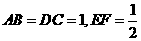 ,则直线
,则直线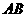 与
与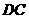 所成的角大小为
所成的角大小为
15
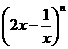 的展开式的二项式系数之和为64,则展开式中常数项为
的展开式的二项式系数之和为64,则展开式中常数项为 
16.若M是直线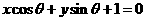 上到原点的距离最近的点,则当
上到原点的距离最近的点,则当 在实数范围内变化时, 动点M的轨迹方程是
。
在实数范围内变化时, 动点M的轨迹方程是
。
12.已知M点为椭圆上一点,椭圆两焦点为F1,F2,且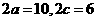 ,点I为
,点I为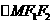 的内心,延长MI交线段F1F2于一点N,则
的内心,延长MI交线段F1F2于一点N,则 的值为( )
的值为( )
(A)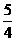 (B)
(B)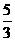 (C)
(C)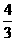 (D)
(D)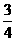

11.已知点P是抛物线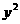 = 2x上的动点,点p在y轴上的射影是M,点A的坐标是
= 2x上的动点,点p在y轴上的射影是M,点A的坐标是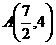 ,则| PA | + | PM |的最小值是
,则| PA | + | PM |的最小值是
(A)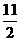 (B)4
(C)
(B)4
(C)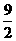 (D)5
(D)5
10.已知等差数列{an}与等差数列{bn}的前n项和分别为Sn和Tn,若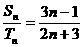 ,则
,则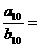
(A)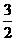 (B)
(B)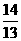 (C)
(C)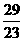 (D)
(D)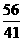
9.从1,2,3,4,5 中取三个不同数字作直线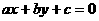 中
中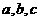 的值,使直线与圆
的值,使直线与圆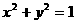 的位置关系满足相离,这样的直线最多有
的位置关系满足相离,这样的直线最多有
(A)30条 (B)20条 (C)18条 (D)12条
8.已知四面体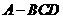 中,
中, 与
与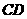 间的距离与
间的距离与
夹角分别为3与 ,则四面体
,则四面体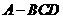 的体积为( )
的体积为( )
(A)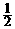 (B)1 (C)2 (D)
(B)1 (C)2 (D)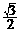
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com