
题目列表(包括答案和解析)
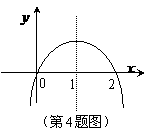
4. 已知函数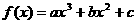 ,其导数
,其导数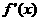 的图象如右图,
的图象如右图,
则函数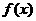 的极小值是
的极小值是
A.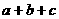 B.
B.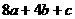 C.
C.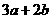 D.
D.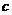
3. 设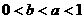 ,则下列不等式成立的是
,则下列不等式成立的是
 A.
A. 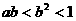 B.
B.
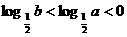
C. 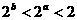 D.
D.
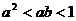
2. 已知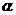 为第二象限的角,且
为第二象限的角,且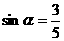 ,则
,则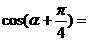
A.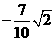 B.
B.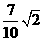 C.
C.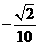 D.
D.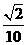
1. 已知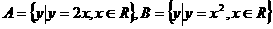 ,则
,则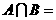
A.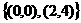 B.
B.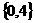 C.
C.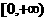 D.
D. 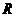
22.(本大题满分14分)在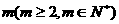 个不同数的排列
个不同数的排列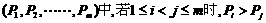 (即前面某数大于后面某数)则称
(即前面某数大于后面某数)则称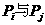 构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,例如排列(2,40,3,1)中有逆序“2与1”,“40与3”,“40与1”,“3与1”其逆序数等于4. 已知n+2
构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,例如排列(2,40,3,1)中有逆序“2与1”,“40与3”,“40与1”,“3与1”其逆序数等于4. 已知n+2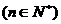 个不同数的排列
个不同数的排列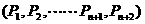 的逆序数是2.
的逆序数是2.
(1)求(1,3,40,2)的逆序数;
(2)写出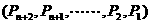 的逆序数an
的逆序数an
(3)令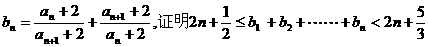 .
.
21.(本大题满分12分)如图,已知椭圆C: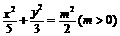 ,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
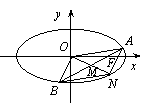 (I)是否存在K,使对任意m>0,总有
(I)是否存在K,使对任意m>0,总有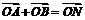 成立?若存在,求出所有K的值;
成立?若存在,求出所有K的值;
(II)若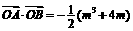 ,求实数k的取值范围.
,求实数k的取值范围.
20.(本大题满分12分)若函数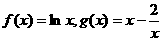
(1)求函数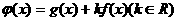 的单调区间
的单调区间
(2)若对所有的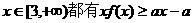 成立,求实数a的取值范围.
成立,求实数a的取值范围.
19.(本大题满分12分)正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B(如图(2))
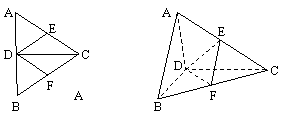

(图1) (图2)
在图形(2)中:
(I)求证:AB∥平面DEF;(II)求二面角E-DF-C的余弦值;
(III)在线段BC上是否存在一点P,使AP⊥DE?说明你的结论.
18.(本大题满分12分)某工厂举行羽毛球选拔赛,由三个车间各推荐两名员工,将这六名员工平均分成3组进行比赛。
(1)求有且只有一个组的两名员工来自同一车间的概率
(2)设有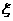 个组的两名员工来自同一车间,求
个组的两名员工来自同一车间,求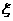 的分布列和期望.
的分布列和期望.
17.(本大题满分12分)已知函数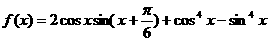
(1)求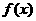 的最小正周期;
的最小正周期;
(2)若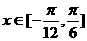 ,求
,求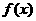 的最大值、最小值及相应的x的值。
的最大值、最小值及相应的x的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com