
题目列表(包括答案和解析)
如图,有两个平面α与β,分别作
 这两个平面的法向量
这两个平面的法向量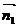 与
与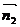 ,则平
,则平

 面α与β所成的角跟法向量
面α与β所成的角跟法向量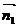 与 α
与 α 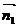
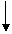



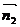 所成的角相等或互补,所以首先
所成的角相等或互补,所以首先
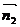 β
β
 必须判断二面角是锐角还是钝角。
必须判断二面角是锐角还是钝角。
例6、如下图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=a,AD=3a,sin∠ADC=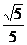 ,且PA⊥平面ABCD,PA=a,求二面角P-CD-A的平面角的余弦值。
,且PA⊥平面ABCD,PA=a,求二面角P-CD-A的平面角的余弦值。

 分析:依题意,先过C点CE⊥AD,计算得ED=2a,BC=AE=a,建立如图右角直角坐标系,则P(0,0,a),D(0,3a,0), P
分析:依题意,先过C点CE⊥AD,计算得ED=2a,BC=AE=a,建立如图右角直角坐标系,则P(0,0,a),D(0,3a,0), P
C(a,a,0),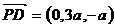 ,
A
E
D
,
A
E
D





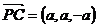 ,
,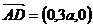 ,
B
C
,
B
C


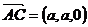
取平面ACD的一个法向量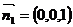 ,设平面PCD的法向量是、
,设平面PCD的法向量是、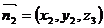 ,所以得
,所以得

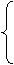
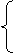
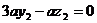
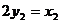
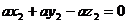
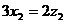 所以不妨取得
所以不妨取得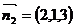 ,从而计算得
,从而计算得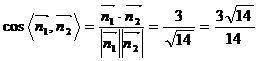
易得二面角P-CD-A的平面角是锐角,所以其角的余弦是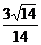
首先必须确定两个平面是否平行,这时可以在一个平面上任取一点,将两平面间的距离问题转化成点到平面的距离问题。
例5、
棱长为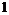 的正方体
的正方体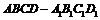 中.求证:平面AB1C∥平面
中.求证:平面AB1C∥平面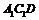 ;
;
(1)
 求平面
求平面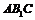 与平面
与平面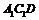 间的距离.
间的距离.
分析(2):建立如图所示的直角坐标系,
则A、D、A1、C1的坐标分别是
(1,0,0)、(0,0,0)、(1,0,1)、
(0,1,1),∴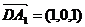 ,
,
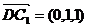 ,
,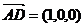 ,将平面
,将平面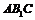 与平面
与平面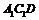 间的距离转化成点A到平面
间的距离转化成点A到平面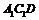 的距离。设平面
的距离。设平面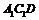 的一个法向量
的一个法向量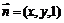 ,
,
则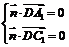 ,即
,即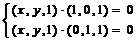
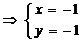 ,
,
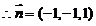 ,
,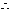 平面
平面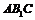 与平面
与平面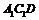 间的距离
间的距离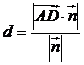
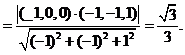
首先必须确定直线与平面平行,然后将直线到平面的距离问题转化成直线上一点到平面的距离问题。
例4、已知边长为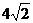 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,求AE与平面α间的距离。
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行,求AE与平面α间的距离。
 分析:因为AE∥平面α,所以将AE与平面α的距离转化成点A到平面α的距离,建立如图右手直角坐标系,
分析:因为AE∥平面α,所以将AE与平面α的距离转化成点A到平面α的距离,建立如图右手直角坐标系,
则A(0,0,0),P(0,0,2),
 E(
E(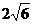 ,0,0),F(
,0,0),F(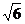 ,
,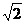 ,0),
P
,0),
P




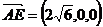
 ,
,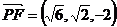 ,
A F
,
A F

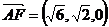 ,设法向量
,设法向量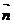 =(x,y,z), B E C
=(x,y,z), B E C
则由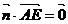 ,
,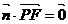 得,
得,
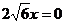
 x=0
x=0
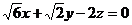
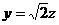 不妨设防z=1,则
不妨设防z=1,则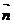 =(0,
=(0,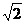 ,1),所以依公式可得所求距离为
,1),所以依公式可得所求距离为
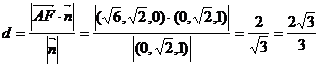

 如右图所示,已知AB是平面α的
如右图所示,已知AB是平面α的


 一条斜线,
一条斜线,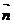 为平面α的法向量,则
C B
为平面α的法向量,则
C B

 A到平面α的距离为
A到平面α的距离为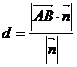 α
α
例3、已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2,求点B到平面EFG的距离。
 分析:建立如图所示右手直角坐标系,
G
分析:建立如图所示右手直角坐标系,
G






 则E(4,-2,0),F(2,-4,0),
E D
则E(4,-2,0),F(2,-4,0),
E D  C
C

 G(0,0,2),B(4,0,0),
A F B
G(0,0,2),B(4,0,0),
A F B
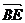 =(0,-2,0),
=(0,-2,0),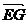 =(-4,2,2),
=(-4,2,2),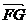 =(-2,4,2),设平面EFG的法向量
=(-2,4,2),设平面EFG的法向量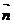 =(x,y,z),则由
=(x,y,z),则由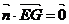 ,
,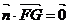 得
得
 -4x+2y+2z=0
x=
-4x+2y+2z=0
x= 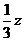
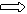 -2x+4y+2z=0
y=
-2x+4y+2z=0
y=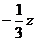
不妨设z=3,则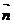 =(1,-1,3),所以依公式可得所求距离为
=(1,-1,3),所以依公式可得所求距离为
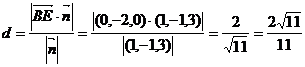


 如右图所示,a、b是两异面直线,
如右图所示,a、b是两异面直线,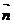 是 a E
是 a E
a和b 的法向量,点E∈a,F∈b,则
 异面直线
a与b之间的距离是
异面直线
a与b之间的距离是
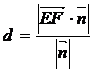 b F
b F
 例1、如下图,正四棱锥S-ABCD的高SO=2,底边长
例1、如下图,正四棱锥S-ABCD的高SO=2,底边长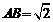 ,求异面直线BD和SC之间的距离.
,求异面直线BD和SC之间的距离.
分析:建立如图所示的直角坐标系,则
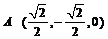 ,
,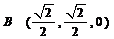 ,
,
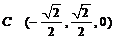 ,
,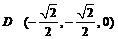 ,
,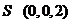 .
.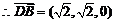 ,
,
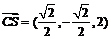 .令向量
.令向量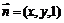 ,且
,且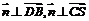 ,则
,则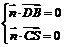 ,
,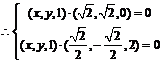 ,
,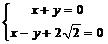 ,
,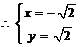 ,
,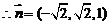 .
.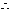 异面直线BD和SC之间的距离为:
异面直线BD和SC之间的距离为:
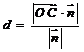
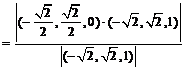
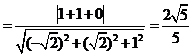 .
.
例2、如下图,正方体ABCD- A1B1C1D1的棱长为2,M、N分别为AA1,BB1的中点,
求(1)CM与D1N的余弦值;
(2)异面直线CM与D1N的距离。(2004年广州调研试题)
 分析(2):建立如图所示右手直角坐标系,则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)
分析(2):建立如图所示右手直角坐标系,则C(0,2,0)、D1(0,0,2)、M(2,0,1)、N(2,2,1)







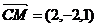 ,
,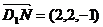 D1
C1
D1
C1


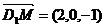 设法向量
设法向量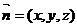 A1 B1
A1 B1




 则 2x-2y+z=0 x=0
M
D
N C
则 2x-2y+z=0 x=0
M
D
N C
2x+2y-z=0 z=2y A B
 令y=1得
令y=1得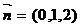 ,依公式得异面直线CM与D1N的距离是
,依公式得异面直线CM与D1N的距离是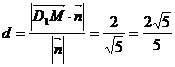
4、 求直线和平面所成的角
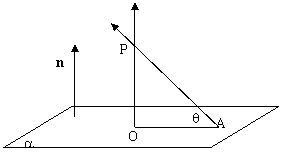
如图,已知PA为平面a的一条斜线,n为平面a的一个法向量,过P作平面a的垂线PO,连结OA则ÐPAO为斜线PA和平面a所成的角记为q,易得
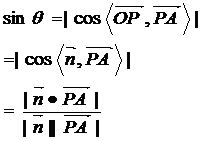
5 、求点到平面的距离
 如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂
如图点P为平面外一点,点A为平面内的任一点,平面的法向量为n,过点P作平面a的垂
线PO,记∠OPA=q,则点P到平面的距离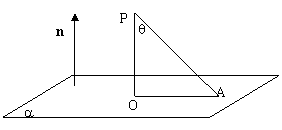
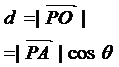
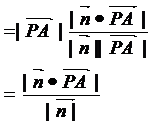
6 、求二面角的大小如图在二面角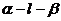 中,n1和n2分别为平面a和b的法向量,若二面角
中,n1和n2分别为平面a和b的法向量,若二面角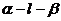 的大小为q,则
的大小为q,则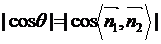 =
=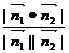 (依据两平面法向量的方向或实际图形来确定q是锐角或是钝角)。
(依据两平面法向量的方向或实际图形来确定q是锐角或是钝角)。
3、求直线和直线所成的角 若直线AB、CD所成的角是a,cosa=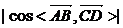
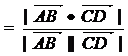
2、 证明面面垂直 验证两个平面的法向量的数量积是否为零。
1、 证明线面平行 取和直线平行的向量,验证该向量和法向量的数量积是否为零。
例4.过正方形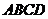 的顶点A,引
的顶点A,引 ,若
,若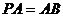 ,
,
则平面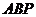 与平面
与平面
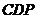 所成的二面角的大小.
所成的二面角的大小.
解:以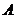 为原点,
为原点,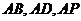 分别为
分别为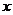 轴
轴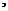
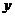 轴,
轴,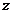 轴建立空间直角坐标系如图。
轴建立空间直角坐标系如图。
则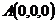 ,
,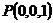 ,
, 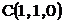 ,
, 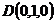 ,则
,则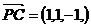 ,
,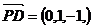 .设平面PCD的法向量为
.设平面PCD的法向量为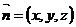 ,
,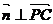 ,即
,即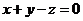 ;
;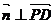 ,即
,即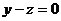 .所以可令
.所以可令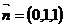 ;设平面PAB的法向量为
;设平面PAB的法向量为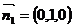 ,所以平面PAB与平面PCD所成的二面角的余弦值为
,所以平面PAB与平面PCD所成的二面角的余弦值为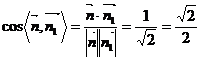 .所以平面
.所以平面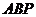 与平面
与平面
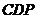 所成的二面角的平面角为
所成的二面角的平面角为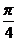 .
.
既然可以利用两个平面的法向量求两平面的夹角,也可以利用两个平面法向量证明两平面垂直.如下面的例5.可以先求两平面的法向量,再计算它们的数量积.
 例5.如图,正四棱柱
例5.如图,正四棱柱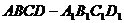 中,底面边长为
中,底面边长为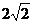 ,侧棱长为4,
,侧棱长为4,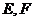 分别为棱
分别为棱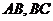 的中点.
的中点.
求证:平面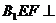 平面
平面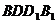
 解:以
解:以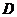 为原点,
为原点,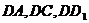 分别
分别
为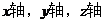 建立空间直角坐标系,则
建立空间直角坐标系,则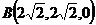 ,
,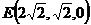 ,
,
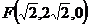
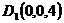
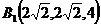
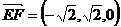
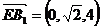
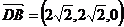 ,
,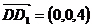 ,
,
设平面EF的法向量为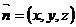 ,
,
则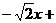
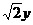 =0;
=0;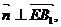 即
即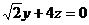 .所以令
.所以令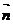 =
=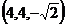
设平面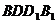 的法向量为
的法向量为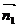 =
=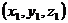 ,
,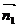
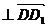 ,即4
,即4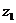 =0;
=0; 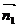
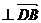 ,即
,即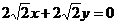 .所以可令
.所以可令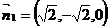 .
.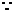
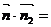
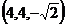
 =0
=0
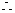 平面
平面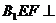 平面
平面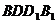 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com