
题目列表(包括答案和解析)
17.(本小题满分12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
(I)在答题卡上完成频率分布表,并在给定的坐标系中画出频率分布直方图;
(II)估计纤度落在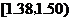 中的概率及纤度小于
中的概率及纤度小于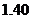 的概率是多少?
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值(例如区间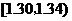 的中点值是
的中点值是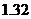 )作为代表.据此,估计纤度的期望.
)作为代表.据此,估计纤度的期望.
14.某篮运动员在三分线投球的命中率是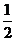 ,他投球10次,恰好投进3个球的概率 .(用数值作答)
,他投球10次,恰好投进3个球的概率 .(用数值作答)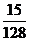
|
分组 |
频数 |
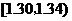 |
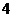 |
 |
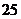 |
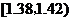 |
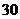 |
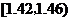 |
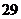 |
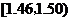 |
 |
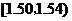 |
 |
|
合计 |
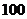 |
9.连掷两次骰子得到的点数分别为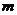 和
和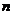 ,记向量
,记向量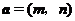 与向量
与向量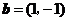 的夹角为
的夹角为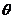 ,则
,则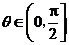 的概率是( )
的概率是( )
A.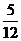 B.
B.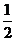 C.
C.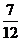 D.
D.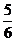
17.解:任选1名下岗人员,记“该人参加过财会培训”为事件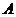 ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件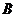 ,由题设知,事件
,由题设知,事件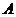 与
与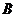 相互独立,且
相互独立,且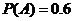 ,
,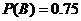 .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
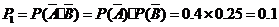
所以该人参加过培训的概率是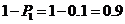 .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是
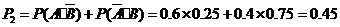
该人参加过两项培训的概率是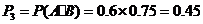 .
.
所以该人参加过培训的概率是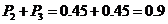 .
.
(II)解法一:任选3名下岗人员,3人中只有2人参加过培训的概率是
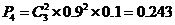 .
.
3人都参加过培训的概率是 .
.
所以3人中至少有2人参加过培训的概率是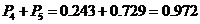 .
.
解法二:任选3名下岗人员,3人中只有1人参加过培训的概率是
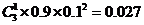 .
.
3人都没有参加过培训的概率是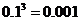 .
.
所以3人中至少有2人参加过培训的概率是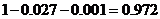 .
.
湖北理
17.(本小题满分12分)
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,求这3人中至少有2人参加过培养的概率.
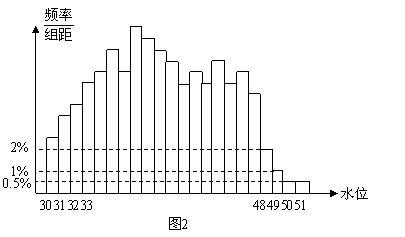
7.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图(如图2).从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是( )
A.48米 B.49米 C.50米 D.51米

17.解:任选1名下岗人员,记“该人参加过财会培训”为事件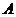 ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件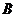 ,由题设知,事件
,由题设知,事件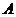 与
与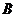 相互独立,且
相互独立,且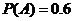 ,
,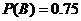 .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
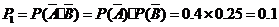
所以该人参加过培训的概率是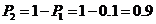 .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是
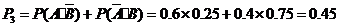
该人参加过两项培训的概率是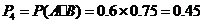 .
.
所以该人参加过培训的概率是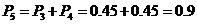 .
.
(II)因为每个人的选择是相互独立的,所以3人中参加过培训的人数 服从二项分布
服从二项分布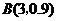 ,
,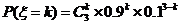 ,
,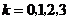 ,即
,即 的分布列是
的分布列是
 |
0 |
1 |
2 |
3 |
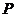 |
0.001 |
0.027 |
0. 243 |
0.729 |
 的期望是
的期望是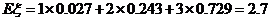 .
.
(或 的期望是
的期望是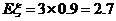 )
)
湖南文
17.(本小题满分12分)
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求 的分布列和期望.
的分布列和期望.
5.设随机变量 服从标准正态分布
服从标准正态分布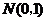 ,已知
,已知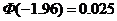 ,则
,则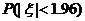 =( )
=( )
A.0.025 B.0.050 C.0.950 D.0.975
17.
解:(1)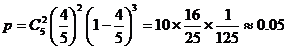
(2)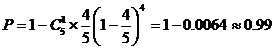
(3)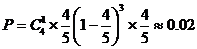
(3)5次预报中恰有2次准确,且其中第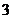 次预报准确的概率;(4分)
次预报准确的概率;(4分)
湖南理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com