
题目列表(包括答案和解析)
2.cos43°cos77°+sin43°cos167°的值为 .
1.命题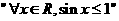 的否定是______________________.
的否定是______________________.
15 (本小题满分13分)
(本小题满分13分)
在等差数列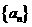 中,
中,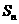 表示数列的前n项和,已知
表示数列的前n项和,已知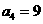 ,
,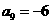 ,求满足
,求满足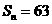 的n值
的n值
16 (本小题满分13分)
(本小题满分13分)
一出租车司机开车从饭店到火车站,途中要过六个交通岗 假设他在各交通岗遇到红灯这一事件是相互独门的,并且概率都是
假设他在各交通岗遇到红灯这一事件是相互独门的,并且概率都是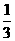

(1) 求这位司机遇到红灯前,连续两个交通岗未遇到红灯的概率;
(2)
求这位司机在途中遇到红灯数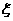 的期望和方差
的期望和方差
17 (本小题满分13分)
(本小题满分13分)
如图,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAB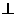 底面ABCD,PA=PB=4,E为PD的中点,过直线BC和点E的平面与棱PA交于点F
底面ABCD,PA=PB=4,E为PD的中点,过直线BC和点E的平面与棱PA交于点F
(1)
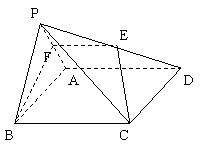 求证:EF
求证:EF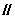 AD
AD
(2)
求直线PC与截面BCEF所成的角
18 (本小题满分13分)
(本小题满分13分)
设函数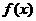 是定义在
是定义在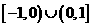 上的奇函数,当
上的奇函数,当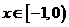 时,
时,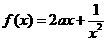
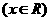

(1)
当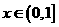 时,求
时,求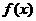 的解析式;
的解析式;
(2)
若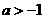 ,试判断
,试判断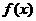 在
在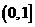 上的单调性,并证明你的结论
上的单调性,并证明你的结论
19 (本小题满分14分)
(本小题满分14分)
今年我市的一个农贸公司计划收购某种农产品,如果按去年各季度该农产品市场价的最佳近似值m收购,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万担 政府为了鼓励收购公司收购这种农产品,决定征收税率降低x个百分点,预测收购量可增加2个百分点
政府为了鼓励收购公司收购这种农产品,决定征收税率降低x个百分点,预测收购量可增加2个百分点
(1) 经计算农贸公司的收购价为m=200(元/担),写出降低征税率后,税收y(万元)与x的函数关系式;;
(2)
要使此项税收值在税率调节后,不少于原计划收购的税收值的83 2%,试确定x的取值范围
2%,试确定x的取值范围
20 (本小题满分14分)
(本小题满分14分)
在平面直角坐标系中,已知 (-3,0)
(-3,0)
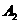 (3,0)
(3,0) P(x,y)
P(x,y) M(
M(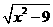 ,0),若实数
,0),若实数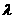 使向量
使向量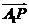

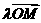

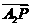 满足
满足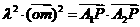
(1) 求P点的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)
当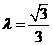 时,过点
时,过点 且斜率为1的直线与(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使
且斜率为1的直线与(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使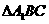 为正三角形
为正三角形
11 复数
复数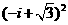 的虚部是
的虚部是

12 若
若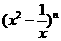 展开式的第6项是x的一次项,那么n=
展开式的第6项是x的一次项,那么n= 
13 曲线C:
曲线C: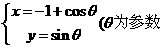 )的普通方程是
,如果曲线C与直线x+m=0有公共点,那么实数m的取值范围是
)的普通方程是
,如果曲线C与直线x+m=0有公共点,那么实数m的取值范围是 
14 如图是某企业近几年来关于生产销售的一张统计图表,则针对该企业近几年的销售情况,有以下几种说法:
如图是某企业近几年来关于生产销售的一张统计图表,则针对该企业近几年的销售情况,有以下几种说法:
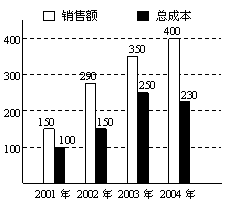 ①这几年该企业的利润逐年提高;(注:利润=销售额-总成本)
①这几年该企业的利润逐年提高;(注:利润=销售额-总成本)
②2001年至2002年是该企业销售额增长最快的一年;
③2002年至2003年是该企业销售额增长最慢的一年;
④2003年至2004年是该企业销售额增长最慢,但是由于总成本有所下降,因而2004年该企业的利润比上一年仍有所增长
其中说法正确的是 (注:把你认为正确的说法的代号都填上)
5.
函数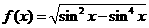 的最小正周期是
的最小正周期是
A 2π B π C 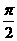 D
D 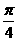
6 若集合A=
若集合A=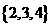 ,B=
,B=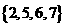 ,从这两个集合中各取一个元素作为平面直角坐标系中点的坐标,能够确定的不同点的个数为
,从这两个集合中各取一个元素作为平面直角坐标系中点的坐标,能够确定的不同点的个数为
A 11 B 12 C 23 D 24
7 已知x
已知x y满足约束条件
y满足约束条件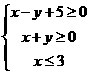 ,则
,则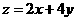 的最小值是
的最小值是
A 5 B -6 C 10 D -10
8 若0<a<1
若0<a<1 0<b<1,且
0<b<1,且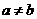 ,则下列各式中值最大的是
,则下列各式中值最大的是
 A
A 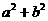 B
B 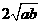 C
C 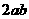 D
D 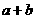
9 已知E
已知E F分别是正方形ABCD的边AB和CD中的中点,沿EF把正方形拆成一个直二面角(如图),则异面直线BF
F分别是正方形ABCD的边AB和CD中的中点,沿EF把正方形拆成一个直二面角(如图),则异面直线BF ED所成角的余弦值为
ED所成角的余弦值为
A 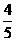 B
B 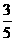 C
C 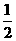 D
D 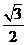
 10
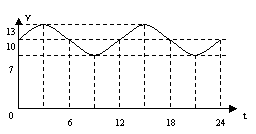
10 某港口水深度y是时间t的函数(0≤t≤24,单位:小时)的函数,记作y=f(t),其曲线可以近似的看成函数y=Asinωt+b的图象(如图),一般情况下船舶航行是,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只须不碰海底即可),某船的吃水深度(船底离水面的距离)为6
某港口水深度y是时间t的函数(0≤t≤24,单位:小时)的函数,记作y=f(t),其曲线可以近似的看成函数y=Asinωt+b的图象(如图),一般情况下船舶航行是,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只须不碰海底即可),某船的吃水深度(船底离水面的距离)为6 5m,如果该船必须在同一天内(24小时)安全进出港,则它能在港口内停留最长的时间为(进出港所需时间忽略不计)
5m,如果该船必须在同一天内(24小时)安全进出港,则它能在港口内停留最长的时间为(进出港所需时间忽略不计)
A 14小时 B 15小时
C 16小时 D 17小时
1.
设全集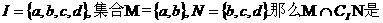
A 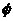 B
B 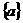 C
C 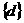 D
D 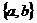
2 不等式
不等式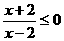 的解集是
的解集是
A 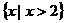 B
B 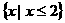 C
C 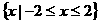 D
D 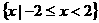
3
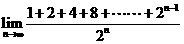 的值等于
的值等于
A 0 B 1 C -1 D 不存在
4 若0<a<1,在区间(-1,0)上函数
若0<a<1,在区间(-1,0)上函数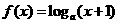 是
是
A增函数且f(x)
>0 B增函数且f(x) <0 C减函数且f(x) >0 D减函数且f(x) >0
7.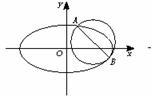 (★★★★★)已知圆C1的方程为(x-2)2+(y-1)2=
(★★★★★)已知圆C1的方程为(x-2)2+(y-1)2=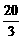 ,椭圆C2的方程为
,椭圆C2的方程为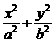 =1(a>b>0),C2的离心率为
=1(a>b>0),C2的离心率为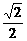 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
6.(★★★★)某抛物线形拱桥跨度是20米,拱高4米,在建桥时每隔4米需用一支柱支撑,求其中最长的支柱的长.
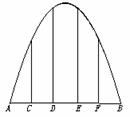
5.(★★★★★)已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|=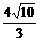 ,试求椭圆的方程.
,试求椭圆的方程.
4.(★★★★)已知圆过点P(4,-2)、Q(-1,3)两点,且在y轴上截得的线段长为4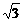 ,则该圆的方程为_________.
,则该圆的方程为_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com