
题目列表(包括答案和解析)
16.(本小题满分12分)
已知向量 a = (cos x,sin x),b = (-cos x,cos x),c = (-1,0)
(I) 若 x = ,求向量 a、c 的夹角;
(II) 当 x∈[,] 时,求函数 f (x) = 2a·b + 1 的最大值。
15.给出下列四个命题:
①过平面外一点,作与该平面成θ角的直线一定有无穷多条;
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定的两条异面直线,过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等;
其中正确的命题序号为 (请把所有正确命题的序号都填上).
14.将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同盒子中的3个中,使得有1个空盒且其它盒子中球的颜色齐全的不同放法共有种.(用数字作答)
13.设f(x)= x2+ax+b,且1≤f(-1)≤2,2≤f(1)≤4,则点(a,b)在aOb平面上的区域面积是
12. 一样本的所有数据分组及频数如下:
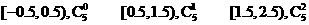
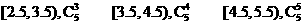
则在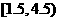 的频率为
的频率为
11.设常数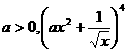 展开式中
展开式中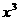 的系数为
的系数为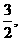 则
则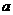 = ______
= ______
10.三位同学在研究函数 f (x) = (x∈R) 时,分别给出下面三个结论: ① 函数 f (x) 的值域为 (-1,1) ② 若x1≠x2,则一定有f (x1)≠f (x2) ③ 若规定 f1(x) = f (x),fn+1(x) = f [ fn(x)],则 fn(x) = 对任意 n∈N* 恒成立. 你认为上述三个结论中正确的个数有( ) (A) 0个 (B) 1个 (C) 2个 (D) 3个
第Ⅱ卷(非选择题 共100分)
9.过抛物线y2 = 2ρx (ρ>0 )上一定点M ( x0,y0
) ( y0≠0 ),作两条直线分别交抛物线于A ( x1 , y1
) , B ( x2 , y2 ),当MA与MB的斜率存在且倾斜角互补时,则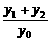 = ( )
= ( )
A.–2 B. 2 C.4 D.– 4
8. 在等差数列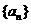 中,
中,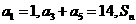 为
为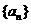 的前
的前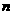 项和,若
项和,若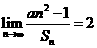 ,则
,则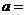 ( )
( )
(A)3 (B) 2 (C)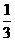 (D)
(D) 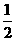
7. 已知△ABC的三个顶点A、B、C及平面内一点P满足: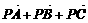 = 0,若实数
= 0,若实数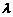 满足:
满足: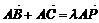 ,则
,则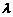 的值为( )
的值为( )
(A)3 (B)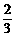 (C)2 (D)8
(C)2 (D)8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com