
题目列表(包括答案和解析)
4.已知x、y满足约束条件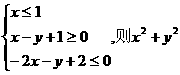 的最小值为
( )
的最小值为
( )
A.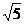 B.
B.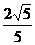 C.1 D.
C.1 D.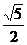
3.已知Sn是等比数列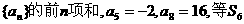 等于
( )
等于
( )
A.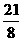 B.-
B.-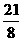 C.
C.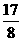 D.-
D.-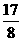
2.已知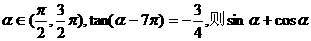 的值为 ( )
的值为 ( )
A.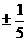 B.
B.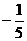 C.
C.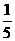 D.
D.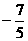
1.已知全集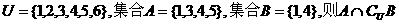 等于( )
等于( )
A.{1,4} B.{2,6} C.{3,5} D.{2,3,5,6}
20、(1)依题意,得: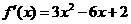 ,
,
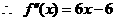 。……………………2分
。……………………2分
由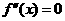 ,即
,即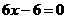 。∴
。∴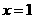 ,又
,又 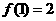 ,
,
∴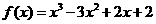 的“拐点”坐标是
的“拐点”坐标是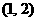 。……………………4分
。……………………4分
(2)由(1)知“拐点”坐标是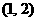 。
。
而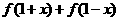 =
=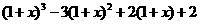
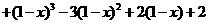
=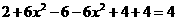 =
=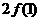 ,
,
由定义(2)知: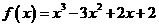 关于点
关于点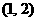 对称。……………………8分
对称。……………………8分
一般地,三次函数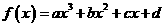
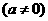 的“拐点”是
的“拐点”是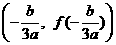 ,它就是
,它就是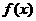 的对称中心。………………………………………………………………………10分
的对称中心。………………………………………………………………………10分
(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数………)都可以给分
(3)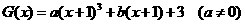 或写出一个具体的函数,如
或写出一个具体的函数,如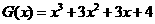 或
或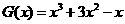 。…………12分
。…………12分
说明:本题在函数、导数、方程的交汇处命题,具有较强的预测性,而且设问的方式具有较大的开放性,情景新颖.解题的关键是:深刻理解函数“拐点”的定义和函数图像的对称中心的意义。其本质是:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;且任何一个三次函数的拐点就是它的对称中心,即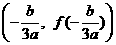 。
。
19、解:∵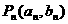 在直线l:y=2x+1,
在直线l:y=2x+1,
∴bn=2an+1……………………0分
∵P1为直线l与y轴交点,
∴P1=(0,1)
∴a1=0……………………2分
又数列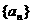 的公差为1
的公差为1
∴an=n-1(n∈N*)……………………4分
∴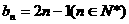
(Ⅱ)∵P1=(0,1),Pn(an,bn)
∴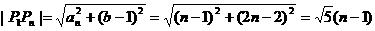 …………………5分
…………………5分
∵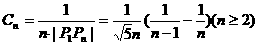 ……………………7分
……………………7分
∴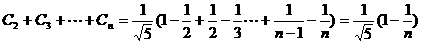 ………8分
………8分
∴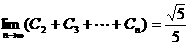 ……………………9分
……………………9分
(Ⅲ)∵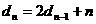
∴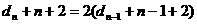 ……………………12分
……………………12分
∴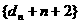 是以2为公比,4为首项的等比数列
是以2为公比,4为首项的等比数列
∴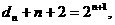
∴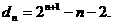 ……………………13分
……………………13分
19、(1)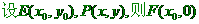
 ,
,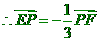 。
。
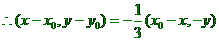 。
。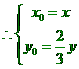 ……… 3分
……… 3分
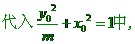
 。
。
 ……… 6分
……… 6分
(2)、
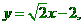
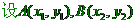 ,
,  。
。
 ,
,
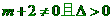 。
。
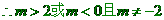 。
………10分
。
………10分
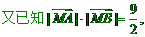
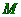 、
、 、
、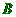
 ,
,
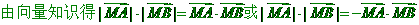 。
。
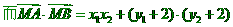
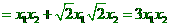 。
。
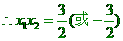 。
。
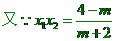 ,
,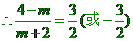 。
。
 。
。
 。
………14 分
。
………14 分
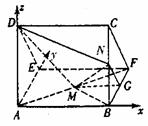
18、18、(本小题满分12分)
解:由三视图可知,该多面体是底面为直
角三角形的直三棱住ADE-BCF,……2分
且AB=BC=BF=2,DE=CF=2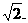
∴∠CBF=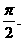 …………………………3分
…………………………3分
(I)取BF中点G,连MG、NG,由M、N分别为AF、BC
的中点可得,NG∥CF,MG∥EF,
∴平面MNG∥平面CDEF,
∴MN∥平面CDEF ………………………………6分
………………………………6分
(II)建立空间直角坐标系,如图,
则A(0,0,0),B(2,0,0),D(0,0,2),F(2,2,0)
M(1,1,0),C(2,0,2),N(2,0,1),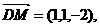
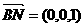 ,
,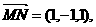 ……………………8分
……………………8分
设平面DMN的法向量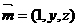
则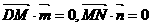 ,
,
则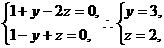
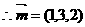 ;……………………………………………………………………9分
;……………………………………………………………………9分
设平面MNB的法向量为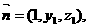
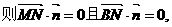
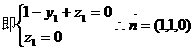 …………………………………………………10分
…………………………………………………10分
设二面角D-MN-B的平面角为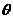 ,则
,则
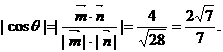
∴二面角D-MN-B的余弦的绝对值为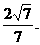 ……………………………………12分
……………………………………12分
17、解:因为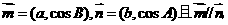
所以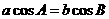 ,-------------------------------------------1分
,-------------------------------------------1分
由正弦定理,得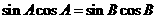 ,
,
即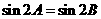 -------------------------------------------------2分
-------------------------------------------------2分
又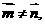 所以
所以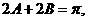 即
即
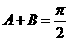 .--------------------------------------------------------3分
.--------------------------------------------------------3分
(1)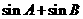 =
=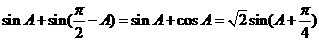 ------4分
------4分
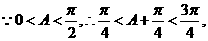
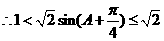
因此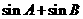 的取值范围是
的取值范围是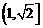 -----------------------------6分
-----------------------------6分
(2)若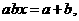 则
则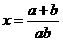 ,
,
由正弦定理,得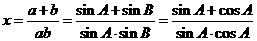 --------------8分
--------------8分
设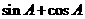 =
=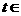
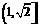 ,则
,则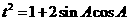 ,
,
所以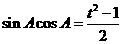 -------------------------------------------10分
-------------------------------------------10分
即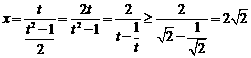
所以实数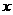 的取值范围为
的取值范围为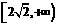 .----------------------------------12分
.----------------------------------12分
16、(Ⅰ)记“甲计算机考试获得合格证书”为事件A,记“乙计算机考试获得合格证书”为事件B,记“丙计算机考试获得合格证书”为事件C,则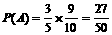 ,
,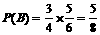 ,
,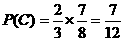 ,有
,有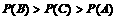 ,故丙获得“合格证书”可能性最大; ……3分
,故丙获得“合格证书”可能性最大; ……3分
(Ⅲ)(理科)用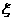 表示甲、乙、丙三人在理论考核中合格人数,则
表示甲、乙、丙三人在理论考核中合格人数,则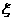 可以取0,1,2,3,故
可以取0,1,2,3,故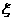 的分布列如下:
的分布列如下:
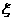 |
0 |
1 |
2 |
3 |
P(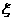 ) ) |
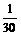 |
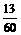 |
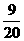 |
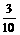 |
……10分
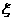 的数学期望:
的数学期望:
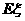 =0×
=0×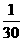 +1×
+1×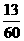 +2×
+2×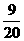 +3×
+3×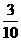 =
=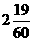 …………………12分
…………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com