6．(2006浙江)设f(x)=3ax²+2bx+c,若a+b+c=0, ,f(0)＞0，f(1)＞0，求证：

　(Ⅰ)a＞0且-2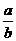＜＜-1；(Ⅱ)方程f(x)=0在(0，1)内有两个实根．

4　　　　 创新试题

5． 已知二次函数y=f₁(x)的图象以原点为顶点且过点(1，1)，反比例函数y=f₂(x)的图象与直线y=x的两个交点间的距离为8，f(x)=f₁(x)+f₂(x)．

(1)求函数f(x)的表达式；

(2)证明：当a＞3时，关于x的方程f(x)=f(a)有三个实数解．

4． 已知acosα+bsinα=c, acosβ+bsinβ=c(ab≠0,α–β≠kπ, k∈Z)求证：

．

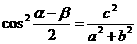3．(2006春上海) 设函数．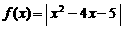

(1)在区间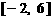上画出函数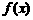的图像；

(2)设集合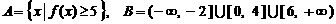． 试判断集合和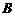之间的关系，并给出证明；

(3)当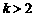时，求证：在区间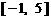上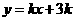，的图像位于函数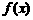图像的上方．

2．求函数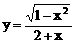的最大值。

1．若不等式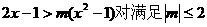的所有m都成立。求x的取值范围。

4． 设奇函数f(x)的定义域为(-∞，0)∪(0，+∞)且在(0，+∞)上单调递增，f(1)＝0，则不等式f［x(x-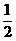)］＜0的解集是______________

3　　　　 解答题

3．(2006湖北)关于x的方程(x²-1)²-|x²-1|+k=0，给出下列四个命题：

①存在实数k，使得方程恰有2个不同的实根

②存在实数k，使得方程恰有4个不同的实根

③存在实数k，使得方程恰有5个不同的实根

④存在实数k，使得方程恰有8个不同的实根

其中假命题的个数是________

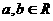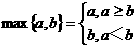2．(2006浙江)对,记则则函数

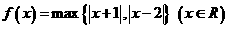的最小值是　．

1．若关于x的方程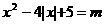有四个不相等的实根，则实数m的取值范围为____。