
题目列表(包括答案和解析)
3.(★★★★★)(4cosθ+3–2t)2+(3sinθ–1+2t)2,(θ、t为参数)的最大值是 .
2.(★★★★★)已知f(x)=(x–a)(x–b)–2(其中a<b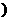 ,且α、β是方程f(x)=0的两根(α<β
,且α、β是方程f(x)=0的两根(α<β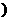 ,则实数a、b、α、β的大小关系为( )
,则实数a、b、α、β的大小关系为( )
A.α<a<b<β B.α<a<β<b
C.a<α<b<β D.a<α<β<b
1.(★★★★)方程sin(x–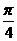 )=
)=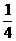 x的实数解的个数是( )
x的实数解的个数是( )
A.2 B.3 C.4 D.以上均不对
3.注意知识间的联系、综合与交汇,提倡一题多问,一题多解,多题一解,培养发散思维和归纳概括的习惯,重视数学思想方法在解综合题中的指导作用。
2.加强作图能力的训练,解题先想图,以图助解题,养成数形结合的习惯;
1.加强对数学概念的复习,深刻理解定义以及数、式的几何意义,真正夯实双基;
2.解: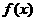 =
=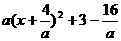 ,∵
,∵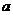 <0∴
<0∴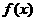 max=
max=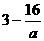
当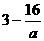 >5,即-8<
>5,即-8<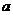 <0时,0<
<0时,0<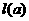 <-
<-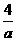 (如图1)
(如图1)
∴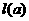 是方程
是方程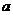 x2+8x+3=5的较小根
x2+8x+3=5的较小根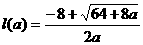 =
=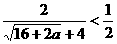
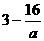 ≤5,即
≤5,即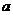 ≤-8时,
≤-8时,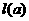 >-
>-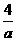 (如图2)
(如图2)
∴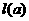 是方程
是方程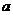 x2+8x+3=-5的较大根
x2+8x+3=-5的较大根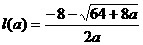 =
=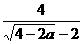
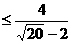 =
=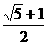 ,当且仅当
,当且仅当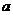 =-8时等号成立,由于
=-8时等号成立,由于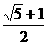 >
>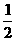 ,
,
因此当且仅当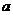 =-8时,
=-8时,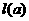 取最大值
取最大值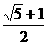 。
。
点评:本题是典型的函数、方程、不等式的综合问题,数形结合利于开拓思路,找到解决办法。
1.解: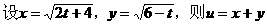
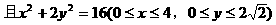
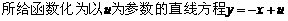 ,
,
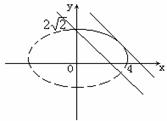
它与椭圆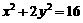 在第一象限的部分(包括端点)有公共点,(如图)
在第一象限的部分(包括端点)有公共点,(如图)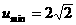
相切于第一象限时,u取最大值
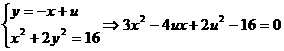
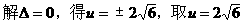
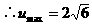
6.证明:(I)因为f(0)>0,f(1)>0,所以c>0,3a+2b+c>0
由条件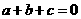 ,消去
,消去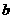 ,得
,得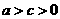 ;
;
由条件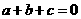 ,消去
,消去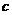 ,得
,得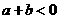 ,
,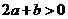 .
.
故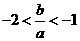 .
.
(II)抛物线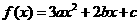 的顶点坐标为
的顶点坐标为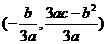 ,
,
在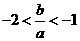 的两边乘以
的两边乘以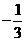 ,得
,得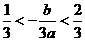 .
.
又因为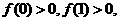
而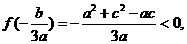
所以方程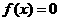 在区间
在区间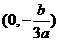 与
与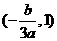 内分别有一实根
内分别有一实根
故方程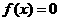 在
在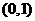 内有两个实根.
内有两个实根.
创新试题
5.分析 用数形结合思想求f(x)-f(a)=0解的个数.
解 (1)由已知,设f1(x)=bx2,由f1(x)=1, 得b=1.∴f1(x)=x2.
设f2(x)=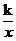 (k>0),则其图象与直线y=x的交点分别为A(k,k),B(-k,-k),由|AB|=8,得k=8,
(k>0),则其图象与直线y=x的交点分别为A(k,k),B(-k,-k),由|AB|=8,得k=8,
∴f2(x)=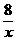 ,故f(x)=x2+
,故f(x)=x2+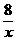 .
.
(2)由f(x)=f(a),得x2+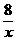 =a2+
=a2+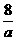 ,
,
即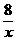 =-x2+a2+
=-x2+a2+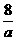 .
.
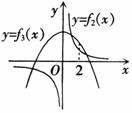
在同一坐标系内作出f2(x)=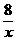 和f3(x)=-x2+a2+
和f3(x)=-x2+a2+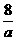 的大致图象(如图所示),其中f2(x)的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,f3(x)的图象是以(0,a2+
的大致图象(如图所示),其中f2(x)的图象是以坐标轴为渐近线,且位于第一、三象限的双曲线,f3(x)的图象是以(0,a2+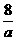 )为顶点,开口向下的抛物线.f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.
)为顶点,开口向下的抛物线.f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.
又∵f2(2)=4,f3(2)=-4+a2+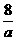 ,当a>3时,
,当a>3时,
f3(2)-f2(2)=a2+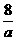 -8>0,
-8>0,
∴当a>3时,在f3(x)第一象限的图象上存在一点(2,f3(2))在f2(x)图象的上方.
∴f2(x)与f3(x)的图象在第一象限有两个交点,即f(x)=f(a)有两个正数解.
故方程f(x)=f(a)有三个实数解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com