3．(本题满分14分)甲与乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次为ξ；乙用这枚硬币掷2次，记正面朝上的次为η.

　 (1)分别求ξ和η的期望；

　 (2)规定；若ξ>η，则甲获胜，若ξ<η，则乙获胜，分别求出甲和乙获胜的概率.

解ξ的可能取值为0，1，2，3则ξ的分布列为

ξ	0	1	2	3

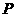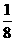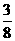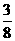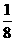则Eξ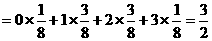

η的可能取值为0，1，2则η的分布列为

η	0	1	2

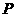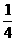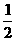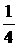则Eη=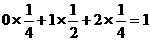

所以ξ、η的数学期望分别为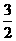、1

(2)P(ξ>η)=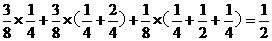

　　 P(ξ<η)=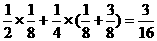

所以甲获胜的概率为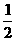，乙获胜的概率为。

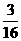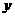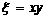2．_{有3张形状、大小、质量完全相同的卡片，在各张卡片上分别标上0、1、2。现从这3张卡片中任意抽出一张，读出其标号，然后把这张卡片放回去，再抽一张，其标号为，记。(1)求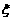的分布列；(2)求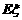和。}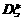

解：(1)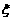_{可能取的值为0、1、2、4。} ……(2分)

_{且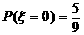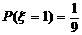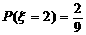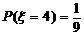，，，　 ……(6分)}

_{所求的分布列为：}

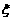	0	1	2	4

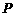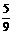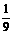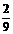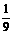_……(8分)

_{(2)由(1)可知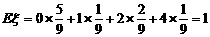，　　　　　　　 ……(11}分)

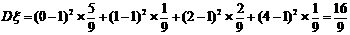_……(14分)

1．解：(1)分布列

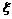	0	1	2	4

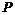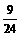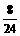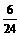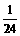(2).

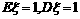1．有同寝室的四位同学分别写一张贺年卡，先集中起来，然后每人去拿一张，设自己拿到自己写的贺卡的人数为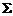，①求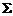的概率分布；②求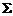的数学期望与方差.

13．甲、乙两名射击运动员，甲射击一次命中10环的概率为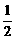，乙射击一次命中10环的概率为s，若他们各自独立地射击两次，设乙命中10环的次数为ξ，且ξ的数学期望Eξ=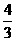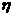，表示甲与乙命中10环的次数的差的绝对值.

　　 (1)求s的值及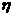的分布列， (2)求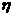的数学期望.

概率解答题练习

12．某中学篮球队进行投篮训练，每人在一轮练习中最多可投篮4次，现规定一旦命中即停止该轮练习，否则一直投到4次为止.已知运动员甲的投篮命中率为0.7.

(1)　　 求一轮练习中运动员甲的投篮次数ξ的分布列，并求出ξ的期望Eξ(结果保留两位有效数字)；

(2)　　 求一轮练习中运动员甲至少投篮3次的概率.

11．学校文娱队的每位队员唱歌、跳舞至少会一项，已知会唱歌的有2人，会跳舞的有5人，现从中选2人．设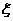为选出的人中既会唱歌又会跳舞的人数，且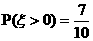．(I) 求文娱队的人数；(II) 写出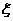的概率分布列并计算．

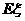10．甲、乙两人参加一次英语口语考试，已知在备选的10道试题中，甲能答对其中6题，乙能答对其中的8题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才算合格。

(Ⅰ)求甲答对试题数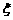的概率分布及数学期望，

(Ⅱ)求甲、乙两人至少有一人考试合格的概率.

9．从分别写有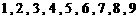的九张卡片中，任意抽取两张，计算：

(Ⅰ)卡片上的数字都是奇数的概率；

(Ⅱ)当两张卡片上的数字之和能被3整除时，就说这次试验成功，求在15次试验中成功次数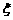的数学期望.

8．袋中有1个白球和4个黑球，每次从其中任取一个球，直到取到白球为止.

(Ⅰ)当每次取出的黑球不再放回时，求取球次数的数学期望与方差；

(Ⅱ)当每次取出的黑球仍放回去时，求取球次数的数学期望与方差.