7.(★★★★★)设数列{a_n}的首项a₁=1，前n项和S_n满足关系式：3tS_n－(2t+3)S_n－1=3t(t＞0,n=2,3,4…).

(1)求证：数列{a_n}是等比数列；

(2)设数列{a_n}的公比为f(t)，作数列{b_n}，使b₁=1,b_n=f(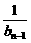)(n=2,3,4…)，求数列{b_n}的通项b_n；

(3)求和：b₁b₂－b₂b₃+b₃b₄－…+b_2n－1b_2n－b_2nb_2n+1.

6.(★★★★★)已知数列{b_n}是等差数列，b₁=1,b₁+b₂+…+b₁₀=145.

(1)求数列{b_n}的通项b_n；

(2)设数列{a_n}的通项a_n=log_a(1+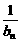)(其中a＞0且a≠1),记S_n是数列{a_n}的前n项和，试比较S_n与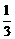log_ab_n+1的大小，并证明你的结论.

5.(★★★★★)设数列{a_n}的前n项和为S_n，且S_n=(m+1)－ma_n.对任意正整数n都成立，其中m为常数，且m＜－1.

(1)求证：{a_n}是等比数列；

(2)设数列{a_n}的公比q=f(m)，数列{b_n}满足：b₁=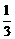a₁,b_n=f(b_n－1)(n≥2,n∈N^*).试问当m为何值时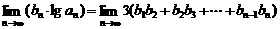，成立？

4.(★★★★)数列{a_n}中，a₁=8,a₄=2且满足a_n+2=2a_n+1－a_n,(n∈N^*).

(1)求数列{a_n}的通项公式；

(2)设S_n=｜a₁｜+｜a₂｜+…+｜a_n｜,求S_n;

(3)设b_n=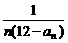(n∈N^*),T_n=b₁+b₂+……+b_n(n∈N^*),是否存在最大的整数m，使得对任意n∈N^*均有T_n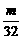＞成立？若存在，求出m的值；若不存在，说明理由.

3.(★★★★)数列{a_n}满足a₁=2，对于任意的n∈N^*都有a_n＞0,且(n+1)a_n²+a_n·a_n+1－

na_n+1²=0，又知数列{b_n}的通项为b_n=2^n－1+1.

(1)求数列{a_n}的通项a_n及它的前n项和S_n；

(2)求数列{b_n}的前n项和T_n；

(3)猜想S_n与T_n的大小关系，并说明理由.

2.(★★★★★)作边长为a的正三角形的内切圆，在这个圆内作新的内接正三角形，在新的正三角形内再作内切圆，如此继续下去，所有这些圆的周长之和及面积之和分别为_________.

1.(★★★★★)设z_n=(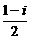)ⁿ，(n∈N^*)，记S_n=｜z₂－z₁｜+｜z₃－z₂｜+…+｜z_n+1－z_n｜，则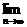S_n=_________.

8.(★★★★★)已知点的序列A_n(x_n，0),n∈N,其中x₁=0,x₂=a(a＞0),A₃是线段A₁A₂的中点，A₄是线段A₂A₃的中点，…，A_n是线段A_n－2A_n－1的中点，….

(1)写出x_n与x_n－1、x_n－2之间关系式(n≥3);

(2)设a_n=x_n+1－x_n，计算a₁,a₂,a₃，由此推测数列{a_n}的通项公式，并加以证明；

(3)求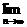x_n.

7.(★★★★)据有关资料，1995年我国工业废弃垃圾达到7.4×10⁸吨，占地562.4平方公里，若环保部门每年回收或处理1吨旧物资，则相当于处理和减少4吨工业废弃垃圾，并可节约开采各种矿石20吨，设环保部门1996年回收10万吨废旧物资，计划以后每年递增20%的回收量，试问：

(1)2001年回收废旧物资多少吨？

(2)从1996年至2001年可节约开采矿石多少吨(精确到万吨)？

(3)从1996年至2001年可节约多少平方公里土地？

6.(★★★★★)某公司全年的利润为b元，其中一部分作为奖金发给n位职工，奖金分配方案如下：首先将职工按工作业绩(工作业绩均不相同)从大到小，由1到n排序，第1位职工得奖金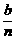元，然后再将余额除以n发给第2位职工，按此方法将奖金逐一发给每位职工，并将最后剩余部分作为公司发展基金.

(1)设a_k(1≤k≤n)为第k位职工所得奖金金额，试求a₂,a₃，并用k、n和b表示a_k(不必证明)；

(2)证明a_k＞a_k+1(k=1,2,…,n－1),并解释此不等式关于分配原则的实际意义；

(3)发展基金与n和b有关，记为P_n(b),对常数b，当n变化时，求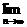P_n(b).