
题目列表(包括答案和解析)
2.(★★★★)已知△ABC中,?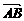 =a,
=a,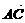 =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=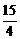 ,|a|=3,|b|=5,则a与b的夹角是( )
,|a|=3,|b|=5,则a与b的夹角是( )
A.30° B.-150° C.150° D.30°或150°
1.(★★★★)设A、B、C、D四点坐标依次是(-1,0),(0,2),(4,3),(3,1),则四边形ABCD为( )
A.正方形 B.矩形
C.菱形 D.平行四边形
16.(人教版84页B组第5题)
试着举几个满足“对定义域内任意实数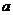 ,
,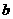 ,都有
,都有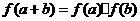 ”的函数例子.
”的函数例子.
变式1:设函数f(x)的定义域是N*,且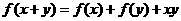 ,
,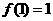 ,则f(25)= ___________________.
,则f(25)= ___________________.
解析:由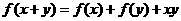
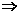
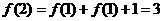
∴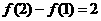
同理,f(3)-f(2)=3.
……
f(25)-f(24)=25.
∴f(25)=1+2+3+…+25=325.
答案:325
变式2:设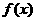 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线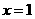 对称,对任意
对称,对任意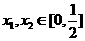 ,都有
,都有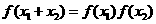
(1)设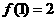 ,求
,求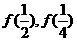
(2)证明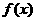 是周期函数.
是周期函数.
(1)解:由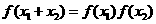 知
知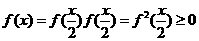 , x∈[0,1].
, x∈[0,1].
因为f(1)=f(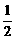 )·f(
)·f(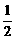 )=[f(
)=[f(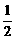 )]2,及f(1)=2,所以f(
)]2,及f(1)=2,所以f(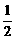 )=2
)=2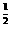 .
.
因为f(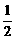 )=f(
)=f(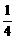 )·f(
)·f(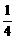 )=[f(
)=[f(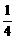 )]2,及f(
)]2,及f(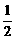 )=2
)=2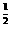 ,所以f(
,所以f(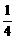 )=2
)=2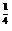 .
.
(2)证明:依题设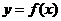 关于直线x=1对称,故f(x)=f(1+1-x)
关于直线x=1对称,故f(x)=f(1+1-x) f(x)=f(2-x),x∈R.
f(x)=f(2-x),x∈R.
又由f(x)是偶函数知f(-x)=f(x),x∈R,所以f(-x)=f(2-x),x∈R.将上式中-x以x代换,得f(x)=f(x+2),x∈R.
这表明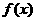 是R上的周期函数,且2是它的一个周期.
是R上的周期函数,且2是它的一个周期.
变式3:设函数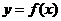 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有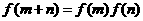 且当
且当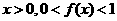
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)|f(x2)·f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,
a∈R},若A∩B=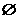 ,求a的取值范围.
,求a的取值范围.
(1)证明:在f(m+n)=f(m)f(n)中,
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1.
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)=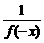 >1.
>1.
(2)证明:设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1.
令m=x1,m+n=x2,则n=x2-x1,代入条件式,得f(x2)=f(x1)·f(x2-x1),
即0<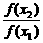 <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).
∴f(x)在R上单调递减.
(3)
解:由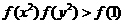
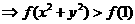
又由(2)知f(x)为R上的减函数,∴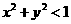
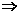 点集A表示圆
点集A表示圆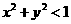 的内部.由f(ax-y+2)=1得ax-y+2=0
的内部.由f(ax-y+2)=1得ax-y+2=0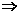 点集B表示直线ax-y+2=0.
点集B表示直线ax-y+2=0.
∵A∩B=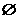 ,∴直线ax-y+2=0与圆
,∴直线ax-y+2=0与圆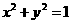 相离或相切。
相离或相切。
于是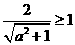
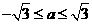
设计意图:考察抽象函数的性质及抽象运算的能力和数形结合的思想。
15.(北师大版第66页B组第3题)
求二次函数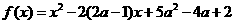 在区间[0,1]上的最小值
在区间[0,1]上的最小值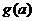 的表达式.
的表达式.
变式1:设a为实数,记函数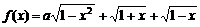 的最大值为g(a).
的最大值为g(a).
(Ⅰ)设t=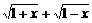 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足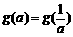 的所有实数a
的所有实数a
解:(I)∵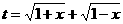 ,
,
∴要使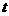 有意义,必须
有意义,必须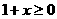 且
且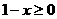 ,即
,即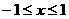
∵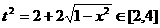 ,且
,且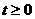 ……① ∴
……① ∴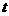 的取值范围是
的取值范围是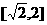 。
。
由①得: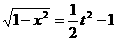 ,∴
,∴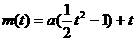
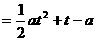 ,
,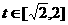 。
。
(II)由题意知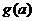 即为函数
即为函数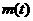
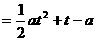 ,
,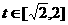 的最大值,
的最大值,
∵直线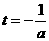 是抛物线
是抛物线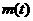
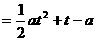 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
(1)当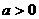 时,函数
时,函数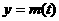 ,
,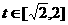 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由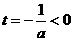 知
知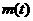 在
在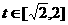 上单调递增,故
上单调递增,故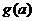
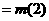
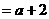 ;
;
(2)当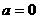 时,
时,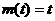 ,
,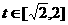 ,有
,有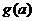 =2;
=2;
(3)当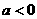 时,,函数
时,,函数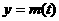 ,
,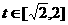 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若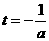
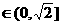 即
即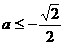 时,
时,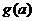
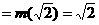 ,
,
若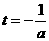
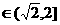 即
即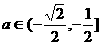 时,
时,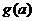
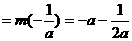 ,
,
若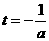
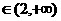 即
即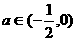 时,
时,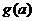
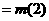
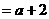 。
。
综上所述,有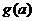 =
=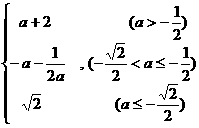 。
。
(III)当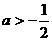 时,
时,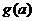
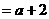
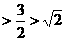 ;
;
当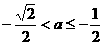 时,
时,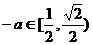 ,
,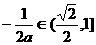 ,∴
,∴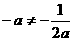 ,
,
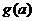
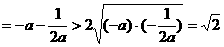 ,故当
,故当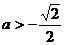 时,
时,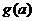
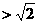 ;
;
当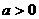 时,
时,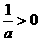 ,由
,由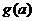
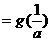 知:
知: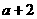
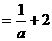 ,故
,故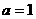 ;
;
当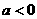 时,
时,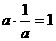 ,故
,故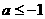 或
或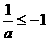 ,从而有
,从而有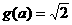 或
或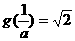 ,
,
要使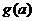
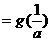 ,必须有
,必须有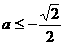 ,
,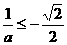 ,即
,即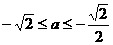 ,
,
此时,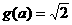
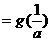 。
。
综上所述,满足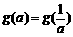 的所有实数a为:
的所有实数a为: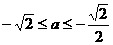 或
或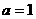 。
。
设计意图:考察二次函数的最值与分类讨论的思想
13.(人教版第49页B组第5题)
证明:
(1)若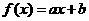 ,则
,则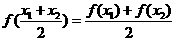
(2)若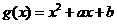 ,则
,则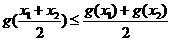
变式1:如图所示,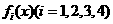 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的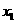 和
和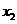 ,任意
,任意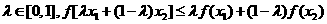 恒成立”的只有 ( )
恒成立”的只有 ( )
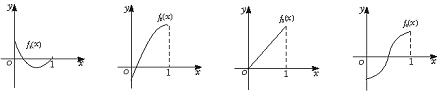
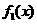
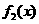
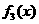
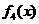
A.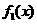 和
和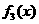 B.
B.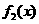 C.
C.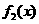 和
和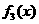 D.
D.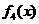
解:当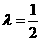 时,符合条件的函数是凹函数,从图像可看出有
时,符合条件的函数是凹函数,从图像可看出有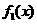 和
和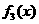 ,选择A.
,选择A.
变式2:.设函数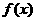 =
=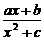 的图象如下图所示,则a、b、c的大小关系是
的图象如下图所示,则a、b、c的大小关系是
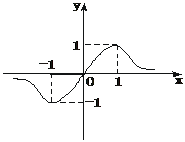
A.a>b>c B.a>c>b C.b>a>c D.c>a>b
解析:f(0)=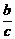 =0,∴b=0.f(1)=1,∴
=0,∴b=0.f(1)=1,∴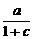 =1.
=1.
∴a=c+1.由图象看出x>0时,f(x)>0,即x>0时,有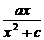 >0,
>0,
∴a>0.又f(x)= 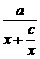 ,
,
当x>0时,要使f(x)在x=1时取最大值1,需x+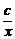 ≥2
≥2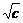 ,
,
当且仅当x=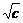 =1时.∴c=1,此时应有f(x)=
=1时.∴c=1,此时应有f(x)=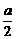 =1.∴a=2.
=1.∴a=2.
答案:B
变式3:如图所示,单位圆中弧AB的长为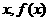 表示弧AB与弦AB
表示弧AB与弦AB
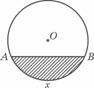 所围成的弓形面积的2倍,则函数
所围成的弓形面积的2倍,则函数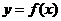 的图象是
的图象是
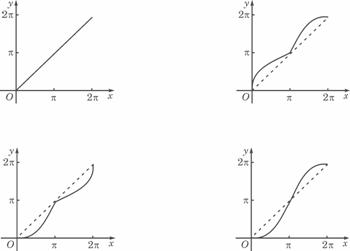
答案:( D )
设计意图:考察图象与式子运算的能力
14:(北师大版136页B组第1题)
判断下列方程在(0,10)内是否存在实数解,并说明理由.
(1)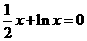 (2)
(2)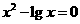
变式1:设二次函数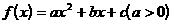 ,方程
,方程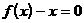 的两个根
的两个根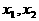 满足
满足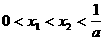 . 当
. 当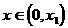 时,证明
时,证明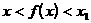 .
.
分析:在已知方程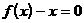 两根的情况下,根据函数与方程根的关系,可以写出函数
两根的情况下,根据函数与方程根的关系,可以写出函数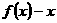 的表达式,从而得到函数
的表达式,从而得到函数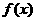 的表达式.
的表达式.
证明:由题意可知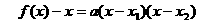 .
.
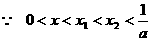 ,
,
∴ 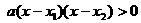 ,
,
∴
当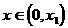 时,
时,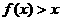 .
.
又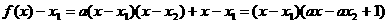 ,
,
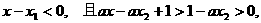
∴
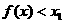 ,
,
综上可知,所给问题获证.
变式2:已知二次函数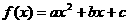 .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)在(1)的条件下,是否存在m∈R,使得f(m)=- a成立时,f(m+3)为正数,若存在,证明你的结论,若不存在,说明理由;
(3)若对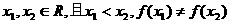 ,方程
,方程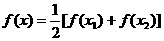 有2个不等实根,
有2个不等实根,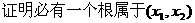
解: (1)
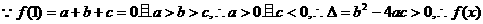
的图象与x轴有两个交点.
(2)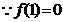 ,∴1是
,∴1是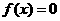 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为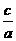 ,
,
∴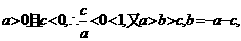
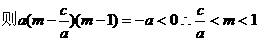
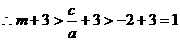
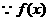 在(1,+∞)单调递增,
在(1,+∞)单调递增,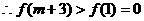 ,即存在这样的m使
,即存在这样的m使
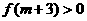
(3)令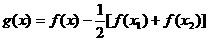 ,则
,则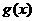 是二次函数.
是二次函数.
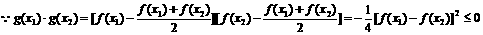
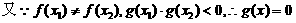 有两个不等实根,且方程
有两个不等实根,且方程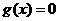 的根必有一个属于
的根必有一个属于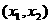 .
.
设计意图:考察函数的零点
12.(人教版48页A组第8题)
设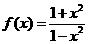 ,求证:(1)
,求证:(1)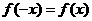 (2)
(2)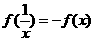
变式1:函数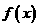 对于任意实数
对于任意实数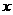 满足条件
满足条件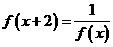 ,若
,若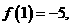 则
则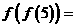 __________.
__________.
解: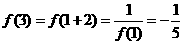 ,
,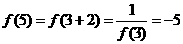 ,又
,又
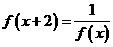 ,∴
,∴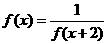 ,
,
∴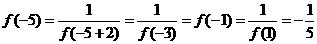
变式2:若奇函数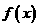
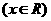 满足
满足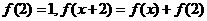 ,则
,则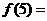
解:由已知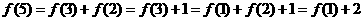 ,令
,令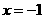 ,则
,则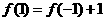 ,又∵
,又∵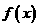 是奇函数,所以
是奇函数,所以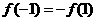 ,
,
∴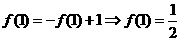 ,∴
,∴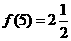
变式3:函数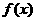 是一个偶函数,
是一个偶函数,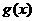 是一个奇函数,且
是一个奇函数,且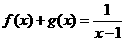 ,则
,则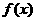 等于
等于
A.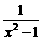 B.
B.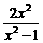 C.
C.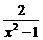 D.
D.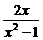
解析:由题知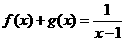 ①
①
以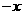 代
代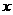 ,①式得
,①式得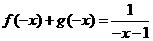 ,即
,即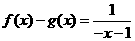 ②
②
①+②得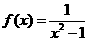
答案:A
设计意图:考察函数的抽象运算与综合性质
11.(人教版65页第8题)
已知下列等式,比较 ,
,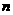 的大小
的大小
(1)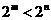 (2)
(2)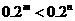
变式1:设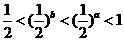 ,那么 ( )
,那么 ( )
A.a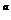 <a
<a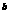 <b
<b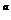 B.a
B.a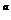 < b
< b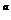 <a
<a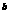
C.a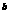 <a
<a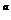 <b
<b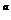 D.a
D.a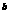 <b
<b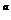 <a
<a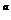
解:由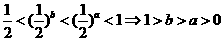 ,在A和B中,
,在A和B中,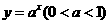 在定义域内是单调递减的,∴
在定义域内是单调递减的,∴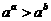 ,所以结论不成立.在C中,
,所以结论不成立.在C中,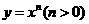 在
在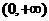 内是单调递增的,又
内是单调递增的,又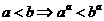 ,所以答案为C.
,所以答案为C.
变式2:已知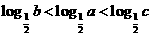 ,则 ( )
,则 ( )
A.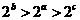 B.
B.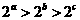
B.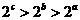 D.
D.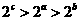
解:由已知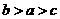 ,因为
,因为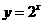 在定义域内是单调递增的,所以
在定义域内是单调递增的,所以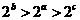
答案为A.
变式3:已知函数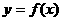 的图象与函数
的图象与函数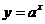 (
(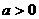 且
且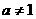 )的图象关于直线
)的图象关于直线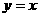 对称,记
对称,记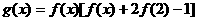 .若
.若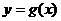 在区间
在区间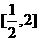 上是增函数,则实数
上是增函数,则实数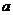 的取值范围是( )
的取值范围是( )
A.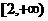 B.
B. C.
C.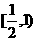 D.
D.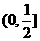
分析:本题根据反函数的定义求出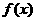 的解析式,再用换元法判断
的解析式,再用换元法判断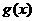 的单调性,结合条件
的单调性,结合条件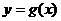 在区间
在区间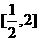 上是增函数,求出实数
上是增函数,求出实数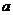 的取值范围是,答案为D
的取值范围是,答案为D
设计意图:考察指、对数函数的单调性
10.(北师大版54页A组第5题)
对于下列函数,试求它们在指定区间上的最大值或最小值,并指出这时的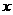 值
值
(2)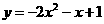 ,
,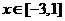
变式1:函数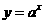 在[0,1]上的最大值与最小值的和为3,则
在[0,1]上的最大值与最小值的和为3,则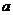 的值为( )
的值为( )
A.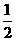 B.2 C.4
D.
B.2 C.4
D.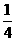
解:当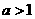 或
或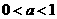 时,函数
时,函数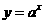 都是定义域上的单调函数,
都是定义域上的单调函数,
∴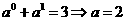 ,故选C.
,故选C.
变式2:若函数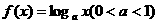 在区间
在区间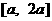 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则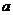 的值为( )
的值为( )
A.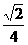 B.
B.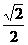 C.
C.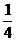 D.
D.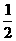
解:∵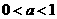 ,∴
,∴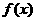 是定义域上的减函数,所以
是定义域上的减函数,所以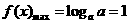 ,
,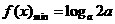 ,∴
,∴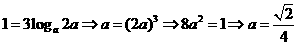 ,故选A
,故选A
设计意图:考察函数的最值
9.(人教版第49页B组第4题)
已知函数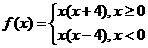 ,求
,求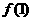 ,
,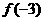 ,
,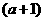 的值
的值
变式1:设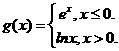 则
则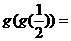 __________
__________
解: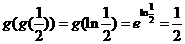 .
.
变式2:已知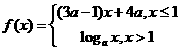 是
是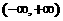 上的减函数,那么
上的减函数,那么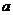 的取值范围是
的取值范围是
A.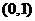 B.
B.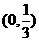
C.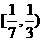 D.
D.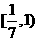
解:分段函数的单调性需分段处理.答案选C
变式3:设函数f(x)=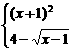
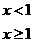 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
解:当x<1时,f(x)≥1 (x+1)2≥1
(x+1)2≥1 x≤-2或x≥0,∴x≤-2或0≤x<1.
x≤-2或x≥0,∴x≤-2或0≤x<1.
当x≥1时,f(x)≥1 4-
4-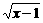 ≥1
≥1
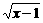 ≤3
≤3 1≤x≤10.
1≤x≤10.
综上,知x≤-2或0≤x≤10.
答案:A
设计意图:考察分段函数的概念和性质
8.(人教版43页B组第3题)
已知函数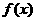 是偶函数,而且在
是偶函数,而且在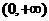 上是减函数,判断
上是减函数,判断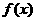 在
在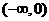 上是增函数还是减函数,并证明你的判断.
上是增函数还是减函数,并证明你的判断.
变式1:下列函数中,在其定义域内既是奇函数又是减函数的是
A. 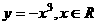 B.
B.
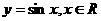
C. 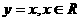 D.
D.
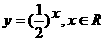
解:B在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定义域内不是奇函数,是减函数;故选A.
变式2:函数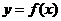 是R上的偶函数,且在
是R上的偶函数,且在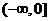 上是增函数,若
上是增函数,若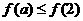 ,则实数
,则实数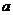 的取值范围是 ( )
的取值范围是 ( )
A.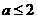 B.
B.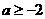 C.
C.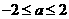 D.
D.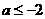 或
或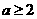
解:当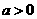 时,∵函数
时,∵函数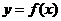 是R上的偶函数,且在
是R上的偶函数,且在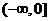 上是增函数,∴
上是增函数,∴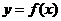 在
在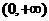 上是减函数,所以若
上是减函数,所以若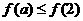 ,则
,则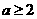 ,当
,当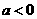 时,函数
时,函数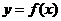 是R上的偶函数,且在
是R上的偶函数,且在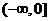 上是增函数,且
上是增函数,且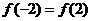 ,∴
,∴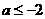 ,故选D
,故选D
设计意图:考察函数奇偶性与单调性的关系
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com