
题目列表(包括答案和解析)
21.(理)已知正项数列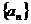 满足对一切
满足对一切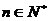 ,有
,有 ,其中
,其中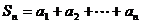 .
.
(Ⅰ)求数列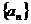 的通项公式;
的通项公式;
(Ⅱ) 求证: 当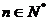 时,
时,  .
.
(文)已知数列{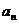 }的前
}的前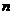 项的和为
项的和为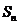 ,对一切正整数
,对一切正整数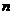 都有
都有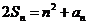 .
.
(1)求数列{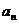 }的通项公式;
}的通项公式;
(2)若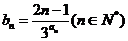 ,证明:
,证明: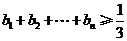 .
.
20. (理)已知函数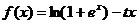 .
.
(Ⅰ)求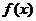 的单调区间;
的单调区间;
(Ⅱ)当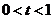 时,记
时,记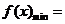
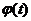 ,求
,求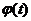 的最大值.
的最大值.
(文)已知函数 .
.
(Ⅰ)若函数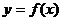 的图象在点P(1,f(1))处的切线的倾斜角为
的图象在点P(1,f(1))处的切线的倾斜角为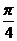 ,求
,求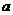 的值;
的值;
(Ⅱ)设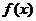 的导函数是
的导函数是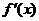 ,在(Ⅰ)的条件下,若m,n
,在(Ⅰ)的条件下,若m,n [﹣1,1],求
[﹣1,1],求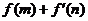 的最小值.
的最小值.
19.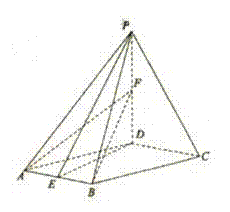 (理)已知四棱锥P-ABCD,底面ABCD是菱形,
(理)已知四棱锥P-ABCD,底面ABCD是菱形,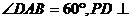 平面ABCD,PD=AD,点E为AB中点,点F为PD中点.
平面ABCD,PD=AD,点E为AB中点,点F为PD中点.
(1)证明平面PED⊥平面PAB;
(2)求二面角P-AB-F的平面角的余弦值
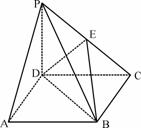 (文)如图,四棱锥
(文)如图,四棱锥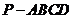 的底面
的底面 是正方形,侧棱
是正方形,侧棱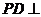 底面
底面 ,
,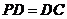 ,
,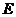 是
是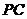 的中点.
的中点.
(Ⅰ)证明 平面
平面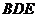 ;
;
(Ⅱ)求二面角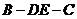 的大小.
的大小.
18.(理)投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,现知某人投入红袋的概率为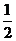 ,投入蓝袋的概率为
,投入蓝袋的概率为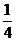 .
.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分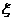 的数学期望及方差.
的数学期望及方差.
(文)投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,现知某人投入红袋的概率为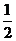 ,投入蓝袋的概率为
,投入蓝袋的概率为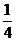 .
.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得2分的概率.
17. (理) 设函数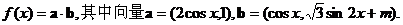
(1)求函数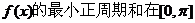 上的单调递增区间;
上的单调递增区间;
(2)当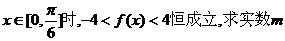 的取值范围。
的取值范围。
(文)在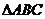 中,
中,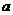 、
、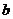 、
、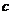 分别为
分别为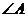 、
、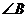 、
、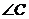 的对边,已知
的对边,已知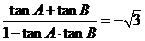 ,
,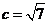 ,三角形面积为
,三角形面积为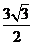 .
.
⑴ 求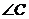 的大小; ⑵ 求
的大小; ⑵ 求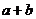 的值.
的值.
16. (理) 现有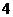 种不同颜色要对如图
种不同颜色要对如图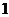 所示的四个部分进行着色,
所示的四个部分进行着色,
要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有
(要求用数字填写).
(文)某餐厅供应盒饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种.现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需要准备不同的素菜 .
15.(理)如图所示,在杨辉三角形中,从上往下数共有n(n∈N*)行,在这些数中非1的数之和为 .
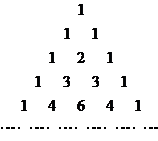
 (文)
(文)  的展开式的二项式系数之和为64,则展开式中常数项为
的展开式的二项式系数之和为64,则展开式中常数项为 
13(理)已知函数 ,且
,且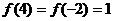 ,
,
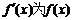 的导函数,函数
的导函数,函数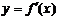 的图象如图所示. 则
的图象如图所示. 则
平面区域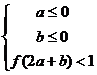 所围成的面积是 .
所围成的面积是 .
(文)已知满足条件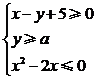 的平面区域的面积是5,则实数
的平面区域的面积是5,则实数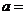 .
.
14.(理)设f(x)=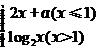 ,若
,若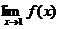 存在,则常数
存在,则常数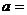 .
.
(文)函数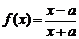 的反函数
的反函数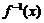 的对称中心为(1,-1),则实数
的对称中心为(1,-1),则实数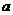 = .
= .
12.在以下命题中:
(1)函数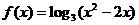 的单调递递减区间是
的单调递递减区间是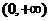 ;
;
(2)函数 的一条对称轴方程是
的一条对称轴方程是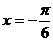 ;
;
(3)已知P: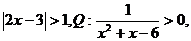 则P是Q的必要不充分条件;
则P是Q的必要不充分条件;
(4) 已知函数 ,方程
,方程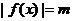 有6个不同的实根,则实数满足
有6个不同的实根,则实数满足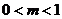 ;
;
(5) 在曲线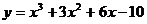 的切线中斜率最小的切线方程是
的切线中斜率最小的切线方程是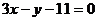 .
.
其中正确命题的序号为( )
A. (3)(4)(5) B.(2)(3)(4) C. (1))(3)(4) D.(2)(4)(5)
11.(理)若向量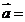 (m,n),
(m,n),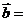 (p,q),且m+n=5,p+q=3,则
(p,q),且m+n=5,p+q=3,则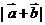 的最小值为
的最小值为
A.4 B.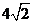 C.
C.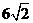 D.8
D.8
(文)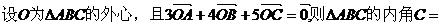 ( )
( )
(A)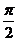 (B)
(B)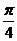 (C)
(C)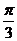 (D)
(D)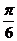
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com