
题目列表(包括答案和解析)
19. (本小题满分16分)
已知数列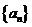 的通项公式为
的通项公式为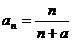 (
(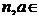 N*).
N*).
(1) 若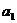 ,
,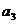 ,
,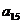 成等比数列,求
成等比数列,求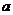 的值;
的值;
(2) 是否存在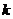 (
(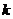 ≥3且
≥3且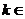 N),使得
N),使得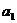 ,
,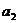 ,
,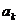 成等差数列,若存在,求出常数
成等差数列,若存在,求出常数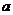
的值;若不存在,请说明理由;
(3) 求证:数列中的任意一项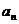 总可以表示成数列中的其他两项之积.
总可以表示成数列中的其他两项之积.
18. (本小题满分16分)
已知直线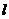 :
: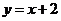 与圆
与圆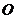 (
(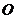 为坐标原点)相切,椭圆
为坐标原点)相切,椭圆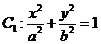
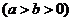
的离心率为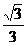 ,短半轴长等于圆
,短半轴长等于圆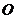 的半径.
的半径.
(1) 求椭圆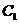 的方程;
的方程;
(2) 抛物线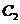 的顶点为原点,焦点为椭圆
的顶点为原点,焦点为椭圆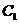 的右焦点,点
的右焦点,点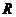 ,
,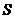 是抛物线
是抛物线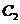 上不同
上不同
的两点,且满足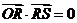 ,求点
,求点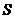 的纵坐标的取值范围.
的纵坐标的取值范围.
17. (本小题满分14分)
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注
意力指数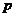 与听课时间
与听课时间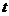 之间的关系满足如图所示的曲线.当
之间的关系满足如图所示的曲线.当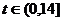 时,曲线是
时,曲线是
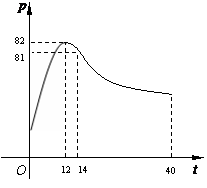
二次函数图象的一部分,当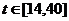 时,曲线是函数
时,曲线是函数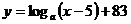 (
(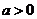 且
且
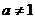 )图象的一部分.根据专家研究,当注意力指数
)图象的一部分.根据专家研究,当注意力指数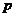 大于80时听课效果最佳.
大于80时听课效果最佳.
(1) 试求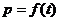 的函数关系式;
的函数关系式;
(2) 老师在什么时段内安排核心内容能使得
学生听课效果最佳?请说明理由.
(第17题)
16. (本小题满分14分)
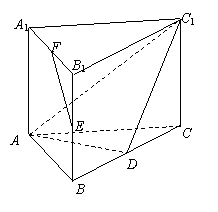 如图,在正三棱柱
如图,在正三棱柱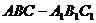 中,点
中,点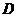 在棱
在棱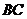 上,
上,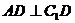 ,点
,点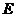 ,
,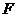 分
分
别是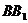 ,
,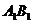 的中点.
的中点.
(1) 求证: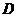 为
为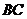 的中点;
的中点;
(2) 求证: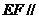 平面
平面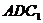 .
.
(第16题)
15. (本小题满分14分)
已知在△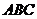 中,
中,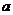 ,
,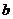 ,
,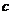 分别为角
分别为角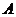 ,
,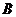 ,
,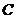 所对的边,
所对的边,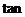 (
(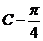 )
)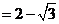 .
.
(1) 求角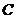 的大小;
的大小;
(2) 若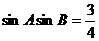 ,试判断△
,试判断△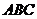 的形状,并说明理由.
的形状,并说明理由.
14. 设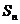 为数列
为数列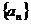 的前
的前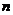 项之和,若不等式
项之和,若不等式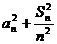 ≥
≥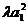 对任意等差数列
对任意等差数列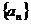 及任意正整数
及任意正整数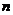 恒成立,则实数
恒成立,则实数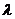 的最大值为 ▲ .
的最大值为 ▲ .
13. 函数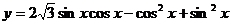 的图象在
的图象在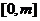 上恰好有两个点的纵坐
上恰好有两个点的纵坐
标为1,则实数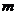 的取值范围是 ▲
.
的取值范围是 ▲
.
12. 用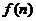 表示自然数
表示自然数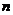 的各位数字的和,例如
的各位数字的和,例如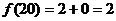 ,
,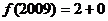
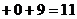 ,若对任意
,若对任意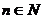 ,都有
,都有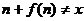 ,满足这个条件的最大的两位
,满足这个条件的最大的两位
数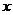 的值是 ▲
.
的值是 ▲
.
11. 若函数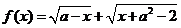 是偶函数,则实数
是偶函数,则实数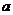 的值为 ▲ .
的值为 ▲ .
10. 已知正四面体的表面积为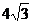 ,则该四面体的体积为 ▲ .
,则该四面体的体积为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com