
题目列表(包括答案和解析)
38.(命题人:南通一中黄健,审题人:南通一中吴勇贫)
已知数列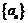 的前n项的和Sn,满足
的前n项的和Sn,满足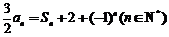 .
.
(1)写出数列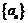 的前3项.
的前3项.
(2)写出数列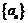 的通项公式.
的通项公式.
(3)设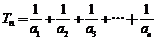 ,是否存在正整数k,使得当n≥3时,
,是否存在正整数k,使得当n≥3时,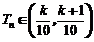 ,如果存在,求出k;如果不存在,请说明理由.
,如果存在,求出k;如果不存在,请说明理由.
解析:(1)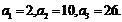
(2)n≥3时,由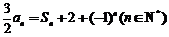 ,得
,得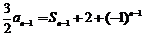 .
.
相减,得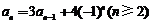 ,
,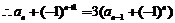 .
.
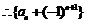 是等比数列.
是等比数列.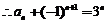 ,
,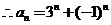 .
.
(3)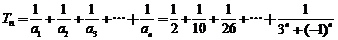 ,
,
当k为偶数时,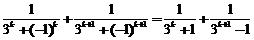
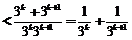 .
.
当n为奇数且n≥3时,
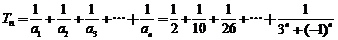
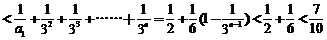 .
.
当n为偶数且n≥3时,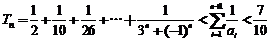 ,
,
所以存在k=6.
37.(命题人:南通中学赵栋,审题人:南通中学杨建楠,原创)
设定义在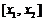 上的函数
上的函数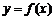 的图象为C,C的端点为点A、B,M是C上的任意一点,向量
的图象为C,C的端点为点A、B,M是C上的任意一点,向量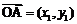 ,
,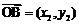 ,
,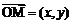 ,若
,若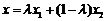 ,记向量
,记向量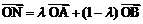 .现在定义“函数
.现在定义“函数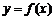 在
在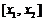 上可在标准k下线性近似”是指
上可在标准k下线性近似”是指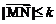 恒成立,其中k是一个人为确定的正数.
恒成立,其中k是一个人为确定的正数.
(1)证明: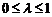 ;
;
(2)请你给出一个标准k的范围,使得[0,1]上的函数y=x2与y=x3中有且只有一个可在标准k下线性近似.
[解析](1)由题意,x1≤x≤x2,即x1≤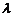 x1+(1-
x1+(1-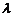 )x2≤x2,∴ x1- x2≤(x1-x2)
)x2≤x2,∴ x1- x2≤(x1-x2)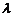 ≤0.
≤0.
∵ x1- x2<0,∴ 0≤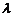 ≤1.
≤1.
(2)由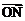 =
=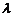
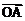 +(1-
+(1-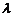 )
)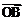 ,得
,得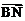 =
=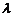
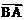 .
.
所以B、N、A三点在一条直线上.
又由(1)的结论,N在线段AB上,且与点M的横坐标相同.
对于 [0,1]上的函数y=x2,A(0,0),B(1,1),
则有|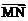 |= x -x2 =
|= x -x2 =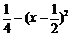 ,故
,故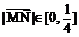 .
.
对于[0,1]上的函数y=x3,则有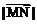 = x-x3= g(x).
= x-x3= g(x).
在(0,1)上, g′(x)= 1-3 x2,
可知在(0,1)上y= g(x)只有一个极大值点x=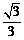 ,
,
所以函数y= g(x)在(0,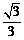 )上是增函数;在(
)上是增函数;在(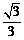 ,1)上是减函数.
,1)上是减函数.
又g(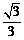 )=
)=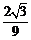 ,故
,故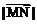
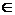 [0,
[0,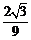 ].
].
经过比较,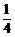 <
<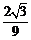 ,所以取k
,所以取k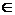 [
[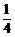 ,
,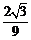 ),则有函数y=x2在[0,1]上可在标准k下线性近似,函数y=x3在[0,1]上不可在标准k下线性近似.
),则有函数y=x2在[0,1]上可在标准k下线性近似,函数y=x3在[0,1]上不可在标准k下线性近似.
36. (命题人:南通中学田宇龙,审题人:南通中学杨建楠,原创)
已知定义域为R的二次函数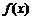 的最小值为0且有
的最小值为0且有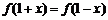 ,直线
,直线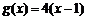 被
被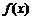 的图像截得的弦长为
的图像截得的弦长为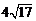 ,数列
,数列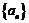 满足
满足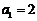 ,
,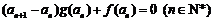 .
.
(1)函数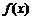 ;
;
(2)求数列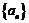 的通项公式;
的通项公式;
(3)设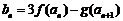 ,求数列
,求数列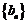 的最值及相应的n.
的最值及相应的n.
[解析](1)设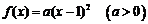 ,
,
则直线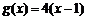 与
与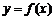 图象的两个交点为(1,0),
图象的两个交点为(1,0),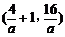 .
.
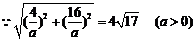 ,
,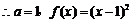 .
.
(2)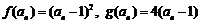 .
.
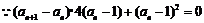 ,
,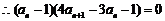 .
.
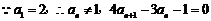 ,
,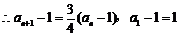 .
.
数列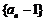 是首项为1,公比为
是首项为1,公比为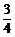 的等比数列,
的等比数列,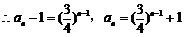 .
.
(3)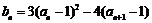
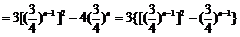 .
.
令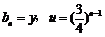 ,则
,则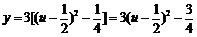 .
.
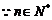 ,
,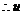 的值分别为
的值分别为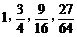 ,…,经比较
,…,经比较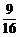 距
距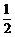 最近,
最近,
∴当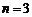 时,
时,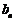 有最小值是
有最小值是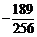 ,当
,当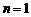 时,
时,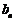 有最大值是0.
有最大值是0.
35.(命题人:如皋市第一中学潘佩,审题人:如皋市第一中学戴圩章)
已知数列
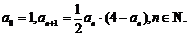
(1)求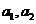 ;
;
(2)证明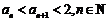 .
.
解:(1)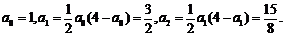
方法一 用数学归纳法证明:
1°
当n=0时,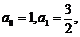 ∴
∴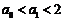 ,命题正确.
,命题正确.
2°
假设n=k时,有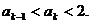
则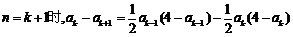
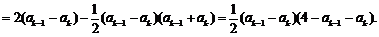
而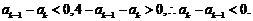
又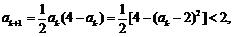 ∴
∴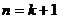 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N,有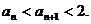
方法二:用数学归纳法证明:
1° 当n=0时,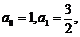 ∴
∴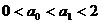 .
.
2° 假设n=k时,有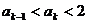 成立,
成立,
令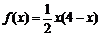 ,
,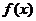 在[0,2]上单调递增,由假设,
在[0,2]上单调递增,由假设,
有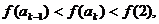 即
即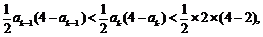
也即当n=k+1时,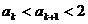 成立,所以对一切
成立,所以对一切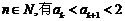 .
.
34.(命题人:如皋市第一中学潘佩,审题人:如皋市第一中学戴圩章)
如图,过点A(6,4)作曲线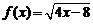 的切线l.
的切线l.
(1)求切线l的方程;
(2)求切线l,x轴及曲线所围成的封闭图形的面积S.
解:(1)∵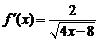 ,∴
,∴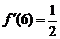 ,∴切线l的方程为
,∴切线l的方程为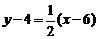 ,即
,即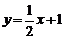 .
.
(2)令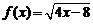 =0,则x=2.令
=0,则x=2.令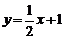 =0,则x= -2.
=0,则x= -2.
∴A=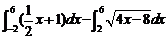 =
=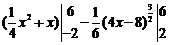 =
=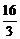 .
.
33.(命题人:如皋市第一中学潘佩,审题人:如皋市第一中学戴圩章)
在平面直角坐标系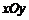 中,抛物线
中,抛物线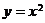 上异于坐标原点O的两不同动点A、B满足
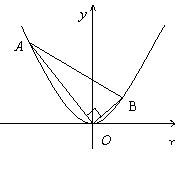
上异于坐标原点O的两不同动点A、B满足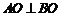 (如图所示),求
(如图所示),求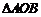 得重心G(即三角形三条中线的交点)的轨迹方程.
得重心G(即三角形三条中线的交点)的轨迹方程.
 解析 法一:∵直线AB的斜率显然存在,
解析 法一:∵直线AB的斜率显然存在,
∴设直线AB的方程为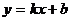 .
.
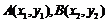 ,依题意,得
,依题意,得
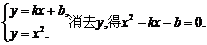 ①
①
∴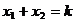 , ②
, ② 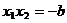 . ③
. ③
∵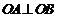 ,∴
,∴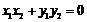 ,即
,即 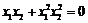 . ④
. ④
由③、④,得 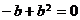 ,∴
,∴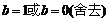 .
.
∴设直线AB的方程为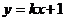 .
.
∴ ①可化为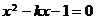 ,∴
,∴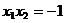 . ⑤
. ⑤
设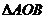 的重心G为
的重心G为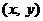 ,则
,则
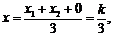 ⑥
⑥ 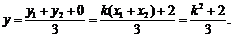 ⑦
⑦
由⑥,⑦,得 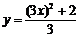 ,即
,即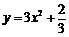 ,这就是
,这就是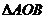 得重心
得重心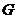 的轨迹方程.
的轨迹方程.
法二:∵ AO⊥BO,直线OA,OB的斜率显然存在,
∴设AO、BO的直线方程分别为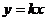 ,
,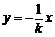 .
.
设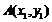 ,
,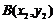 ,依题意,可得
,依题意,可得
由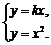 得
得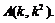 由
由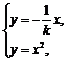 得
得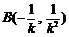 .
.
设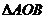 的重心G为
的重心G为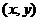 ,则
,则
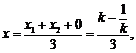 ①
① 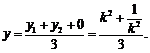 ②
②
由①②,可得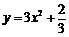 ,即为所求的轨迹方程.
,即为所求的轨迹方程.
法三:(I)设△AOB的重心为G(x,y),A(x1, y1),B(x2,y2 ),则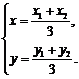 (1)
(1)
∵OA⊥OB ,∴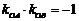 ,即
,即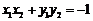 . (2)
. (2)
又点A,B在抛物线上,有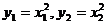 .代入(2)化简,得
.代入(2)化简,得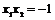 .
.
∴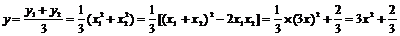 ,
,
∴所以重心为G的轨迹方程为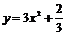 .
.
32.(命题人:如皋市第一中学潘佩,审题人:如皋市第一中学戴圩章)
如图,在四棱锥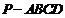 中,底面
中,底面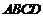 为矩形,侧棱
为矩形,侧棱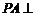 底面
底面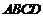 ,
,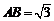 ,
,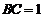 ,
,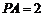 ,E为PD的中点.
,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离.
 解:(Ⅰ)建立如图所示的空间直角坐标系,
解:(Ⅰ)建立如图所示的空间直角坐标系,
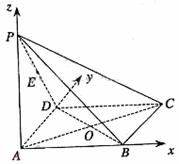
则A,B,C,D,P,E的坐标为A(0,0,0),
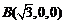 ,
,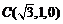 ,
,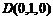 ,
,
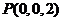 ,
,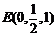 ,
,
从而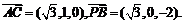
设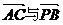 的夹角为
的夹角为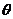 ,则
,则
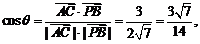
∴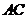 与
与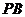 所成角的余弦值为
所成角的余弦值为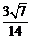 .
.
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为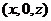 ,则
,则
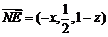 ,由
,由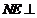 面PAC,可得
面PAC,可得
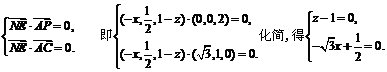 ∴
∴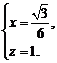
即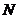 点的坐标为
点的坐标为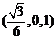 ,从而
,从而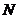 点到
点到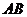 和
和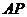 的距离分别为
的距离分别为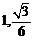 .
.
31.(命题人:如皋市第一中学潘佩,审题人:如皋市第一中学戴圩章)
某次象棋比赛的决赛在甲乙两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分;比赛共进行五局,积分有超过5分者比赛结束,否则继续进行. 根据以往经验,每局甲赢的概率为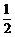 ,乙赢的概率为
,乙赢的概率为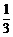 ,且每局比赛输赢互不受影响.若甲第n局赢、平、输的得分分别记为
,且每局比赛输赢互不受影响.若甲第n局赢、平、输的得分分别记为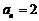 、
、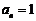 、
、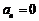
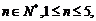 令
令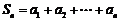 .
.
(Ⅰ)求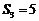 的概率;
的概率;
(Ⅱ)若随机变量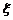 满足
满足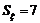 (
(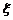 表示局数),求
表示局数),求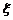 的分布列和数学期望.
的分布列和数学期望.
解:(I)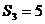 ,即前3局甲2胜1平.由已知,
,即前3局甲2胜1平.由已知,
甲赢的概率为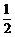 ,平的概率为
,平的概率为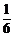 ,输的概率为
,输的概率为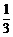 ,∴
,∴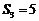 .概率为
.概率为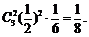
(II)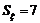 时,
时,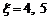 ,且最后一局甲赢,
,且最后一局甲赢,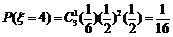 ;
;
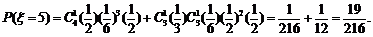
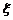 的分布列为
的分布列为
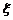 |
4 |
5 |
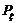 |
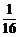 |
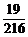 |
∴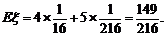
30.(命题人:海门中学方伟,审题人:海门中学沈永飞)
某保险公司新开设了一项保险业务,若在一年内事件E发生,该公司要赔偿a元,设在一年内E发生的概率为p,为使公司收益的期望值等于a的百分之十,公司应要求顾客交多少保险金
解:设保险公司要求赔偿顾客交x元保险金,若以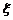 表示公司每年的收益额,则
表示公司每年的收益额,则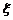 的分布列为
的分布列为
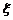 |
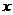 |
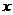 -a -a |
|
p |
1-p |
p |
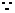 公司每年收益
公司每年收益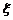 的期望值为:E
的期望值为:E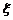 =x(1-p)+(x-p)p=x-ap,
=x(1-p)+(x-p)p=x-ap,
要使公司收益的期望值等于a的10%,只需E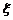 =0.1a,即x-ap=0.1a,x=(0.1+p)a,
=0.1a,即x-ap=0.1a,x=(0.1+p)a,
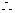 应交的保险金为(0.1+p)a.
应交的保险金为(0.1+p)a.
29.(命题人:海门中学陈达,审题人:海门中学方伟)
已知函数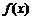 的定义域为R,对任意实数
的定义域为R,对任意实数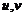 满足
满足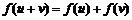 ,且
,且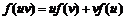 .
.
(1)求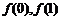 ;
;
(2)试用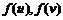 表示
表示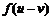 ;
;
(3)用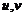 ,
,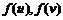 的表达式来表示
的表达式来表示 .
.
答案:(1)利用赋值法易得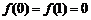 .
.
(2)令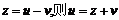 ,由条件,得
,由条件,得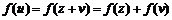 ,所以
,所以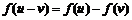 .
.
(3)设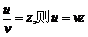 ,由条件,得
,由条件,得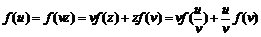 ,
,
所以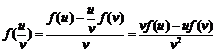 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com