
题目列表(包括答案和解析)
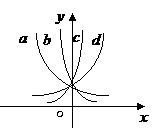
3、如图为指数函数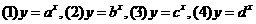 ,则
,则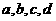 与1的大小关系为
( )
与1的大小关系为
( )
(A)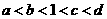 (B)
(B)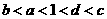
(C)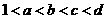 (D)
(D)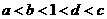
2、已知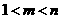 ,令
,令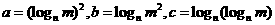 ,则 ( )
,则 ( )
 (A)a<b<c
(B)a<c<b
(C)b<a<c
(D)c<a<b
(A)a<b<c
(B)a<c<b
(C)b<a<c
(D)c<a<b
1、对于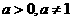 ,下列说法中,正确的是 ( )
,下列说法中,正确的是 ( )
(A)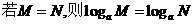 (B)
(B) 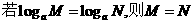
(C) 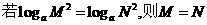 (D)
(D) 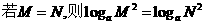
4、以5年真题作为主要复习训练题,引导学生熟悉题型,把握方向,体验难度,领悟高考真题的精妙之处
3、突出向量的工具作用,注重向量与其他知识的综合运用的训练。
2、引导学生对基本公式的变式进行适度拓展,注重基本考点的归纳和应用,如:同角三角函数关系式的变式、两角和的正切公式变式;正弦定理、余弦定理的变式;配角方法;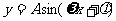 的变换及其对称性质、单调性;辅助函数
的变换及其对称性质、单调性;辅助函数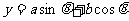 的应用;数量积及其运算性质。
的应用;数量积及其运算性质。
1、立足课本,夯实基础,使学生确实、领会、熟记基本概念、公式和基本运算法则、性质,并在复习中,时刻将这些基础知识渗透落实在解题中,构建知识,体系,形成知识网络。
26.如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为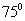 ,
,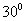 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为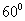 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,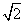
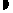 1.414,
1.414,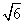
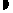 2.449)
2.449)
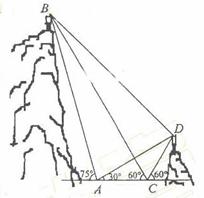
解。在△ABC中,∠DAC=30°, ∠ADC=60°-∠DAC=30,
所以CD=AC=0.1 又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA,
在△ABC中,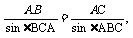
即AB=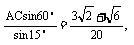
因此,BD=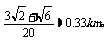
故B,D的距离约为0.33km。
教学启示:
25.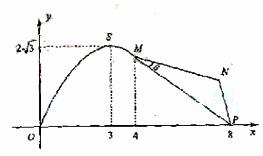 如图,某市拟在长为8km的道路OP的一侧修建一条运
动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
如图,某市拟在长为8km的道路OP的一侧修建一条运
动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数
y=Asin x(A>0,
x(A>0, 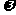 >0) x
>0) x [0,4]的图象,且图象的最高点为
[0,4]的图象,且图象的最高点为
S(3,2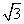 );赛道的后一部分为折线段MNP,为保证参赛
);赛道的后一部分为折线段MNP,为保证参赛
运动员的安全,限定 MNP=120
MNP=120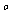
(I)求A , 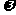 的值和M,P两点间的距离;
的值和M,P两点间的距离;
(II)应如何设计,才能使折线段赛道MNP最长?
.本小题主要考查三角函数的图象与性质、解三角形等基础知识,考查运算求解能力以及应用数学知识分析和解决实际问题的能力,考查化归与转化思想、数形结合思想,
解法一
(Ⅰ)依题意,有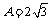 ,
,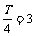 ,又
,又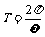 ,
,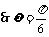 。
。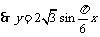
当 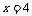 是,
是,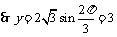
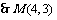 又
又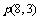
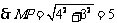
(Ⅱ)在△MNP中∠MNP=120°,MP=5,
设∠PMN=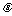 ,则0°<
,则0°<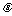 <60°
<60°
由正弦定理得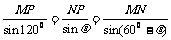
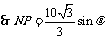 ,
,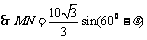
故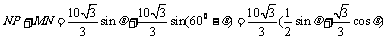
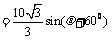
 0°<
0°<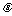 <60°,
<60°,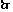 当
当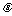 =30°时,折线段赛道MNP最长
=30°时,折线段赛道MNP最长
亦即,将∠PMN设计为30°时,折线段道MNP最长
解法二:
(Ⅰ)同解法一
(Ⅱ)在△MNP中,∠MNP=120°,MP=5,
由余弦定理得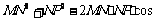 ∠MNP=
∠MNP=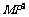
即
故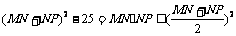
从而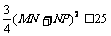 ,即
,即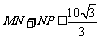
当且仅当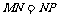 时,折线段道MNP最长
时,折线段道MNP最长
24.在△OAB的边OA、OB上分别有一点P、Q,已知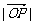 :
: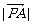 =1:2,
=1:2, 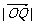 :
: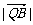 =3:2,连结AQ、BP,设它们交于点R,若
=3:2,连结AQ、BP,设它们交于点R,若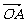 =a,
=a,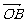 =b.
=b.
(Ⅰ)用a与 b表示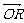 ;
;
(Ⅱ)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角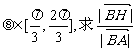 的范围.
的范围.
解:(1)由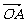 =a,点P在边OA上且
=a,点P在边OA上且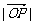 :
: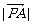 =1:2,
=1:2,
可得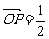 (a-
(a-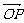 ), ∴
), ∴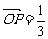 a. 同理可得
a. 同理可得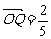 b.
b.
设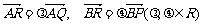 ,
,
则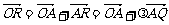 =a+
=a+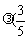 b-a)=(1-
b-a)=(1-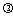 )a+
)a+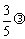 b,
b,
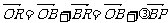 =b+
=b+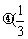 a-b)=
a-b)=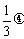 a+(1-
a+(1-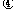 )b.
)b.
∵向量a与b不共线, ∴
∴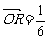 a+
a+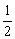 b.
b.
(2)设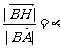 ,则
,则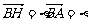 (a-b),
(a-b),
∴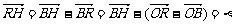 (a-b)- (
(a-b)- (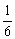 a+
a+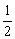 b)+b
b)+b
=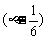 a+(
a+(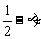 b.
b.
∵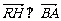 , ∴
, ∴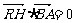 ,即[
,即[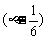 a+(
a+(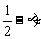 b]·(a-b)=0
b]·(a-b)=0
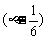 a2+(
a2+(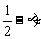 b2+
b2+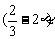 a·b=0
a·b=0
又∵|a|=1, |b|=2, a·b=|a||b|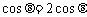 ,
,
∴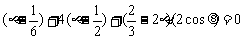
∴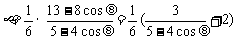 .
.
∵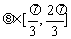 , ∴
, ∴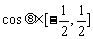 , ∴5-4
, ∴5-4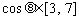 ,
,
∴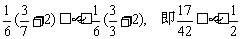 .
.
故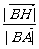 的取值范围是
的取值范围是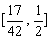 .
.
题型五:三角函数应用
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com