
题目列表(包括答案和解析)
9.(12分)已知函数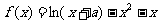 在
在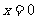 处取得极值,
处取得极值,
(1)求实数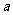 的值;
的值;
(2)若关于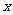 的方程
的方程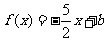 在区间
在区间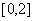 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数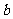 的取值范围.
的取值范围.
8. (12分)已知以点P为圆心的圆过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C、D,且|CD|=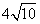 .
.
(1) 求直线CD的方程;
(2)求圆P的方程;
(3)设点Q在圆P上,试探究使△QAB的面积为8的点Q共有几个?证明你的结论.
7.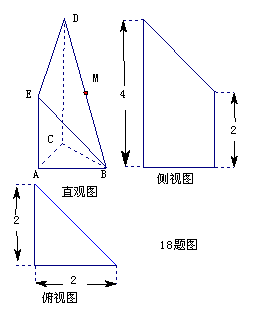 (12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,
(12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,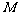 是
是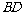 的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
 (1)求出该几何体的体积;
(1)求出该几何体的体积;
 (2)求证:EM∥平面ABC;
(2)求证:EM∥平面ABC;
 (3)试问在棱DC上是否存在点N,使NM⊥平面
(3)试问在棱DC上是否存在点N,使NM⊥平面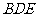 ? 若存在,确定点N的位置;若不存在,请说明理由.
? 若存在,确定点N的位置;若不存在,请说明理由.


18.
(12分)已知数列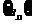 中,
中,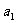 =1,前n项的和为
=1,前n项的和为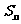 ,对任意的自然数
,对任意的自然数 ,
,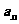 是
是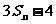 与2-
与2-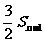 的等差中项.(1)求通项
的等差中项.(1)求通项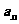 ;(2)求
;(2)求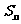 .
.
6.(10分)已知向量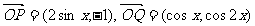 ,定义函数
,定义函数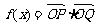 .
.
(1)求函数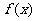 的表达式,并指出其最大最小值;
的表达式,并指出其最大最小值;
(2)在锐角△ABC中,角A,B,C的对边分别为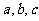 ,且
,且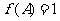 ,
,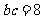 ,
,
求△ABC的面积S. 
5、(本小题满分14分)
已知二次函数f(x)满足f(-1)=0,且 8x f(x)
f(x) 4(x2+1) 对
4(x2+1) 对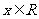 恒成立
恒成立
(1)求函数y=f(x)的解析式;
(2)利用函数g(x)=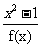 的定义域为D,构造一个数列{xn},方法如下:
的定义域为D,构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2= g(x1),x3=g(x2),…,xn= g(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域D中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
如果X1=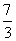 ,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn}
,请求出满足上述条件的数列{xn}的集合M={x1,x2,…,xn} 
3.(本小题满分14分)
已知点A(7,0)在曲线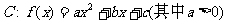 上,且曲线C在点A处的切线与直线
上,且曲线C在点A处的切线与直线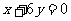 垂直,又当
垂直,又当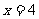 时,函数
时,函数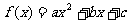 有最小值.
有最小值.
(I)求实数a,b,c的值; 
(II)设函数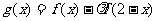 的最大值为M,
的最大值为M,
求正整数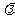 的值,使得
的值,使得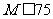 成立.
成立.
4(本小题满分14分)
函数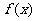 是定义域为R的偶函数,且对任意的
是定义域为R的偶函数,且对任意的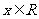 ,均有
,均有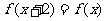 成立.当
成立.当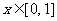 时,
时,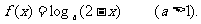
(1)当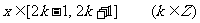 时,求
时,求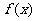 的表达式;
的表达式; 
(2)若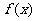 的最大值为
的最大值为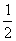 ,解关于x的不等式
,解关于x的不等式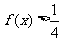 .
.
2. (本小题满分14分)
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,
讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随
后学生的注意力开始分散. 设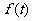 表示学生注意力随时间t(分钟)的变化规律(
表示学生注意力随时间t(分钟)的变化规律(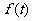
越大,表明学生注意力越集中),经过实验分析得知:
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟? 
(2)有一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么
老师能否在学生达到所需的状态下讲授完这道题目?若能,老师如何安排讲解时
间;若不能,说明理由.
1、(本小题满分12分)
已知函数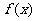 =
=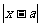 ,
,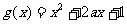 (a为正常数),
(a为正常数),
且函数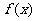 与
与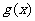 的图象在y轴上的截距相等.
的图象在y轴上的截距相等.
(1)求a的值; 
(2)求函数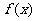 -
-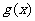 的单调递增区间.
的单调递增区间.
13. (本小题满分14分)
已知函数 ,
,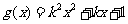 ,
,
其中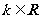 .
.
(I)设函数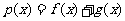 .若
.若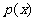 在区间
在区间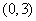 上不单调,求
上不单调,求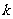 的取值范围;
的取值范围;
(II)设函数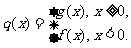 是否存在
是否存在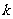 ,对任意给定的非零实数
,对任意给定的非零实数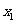 ,存在惟一的非零实数
,存在惟一的非零实数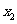 (
(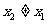 ),使得
),使得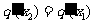 成立?若存在,求
成立?若存在,求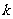 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com