
题目列表(包括答案和解析)
4、数列{an}的通项公式是an=1-2n,其前n项和为Sn,则数列{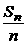 }的11项和为_____
}的11项和为_____
5设函数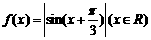 ,则
,则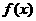 的单调递增区间为
的单调递增区间为
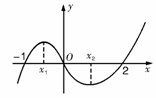
3、如图是函数f(x)=x3+bx2+cx+d的大致图象,则x12+x22等于________.
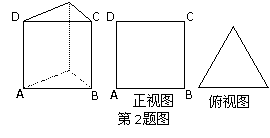
2、如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱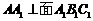 ,正视图是边长为2的正方形,该三棱柱的左视图面积为________.
,正视图是边长为2的正方形,该三棱柱的左视图面积为________.
1、设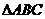 的三个内角
的三个内角 、
、 、
、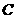 所对边的长分别是
所对边的长分别是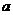 、
、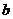 、
、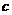 ,且
,且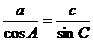 ,
,
那么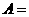
16.设函数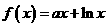 ,
,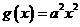 .
.
⑴当 时,求函数
时,求函数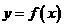 图象上的点到直线
图象上的点到直线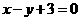 距离的最小值;
距离的最小值;
⑵是否存在正实数 ,使
,使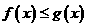 对一切正实数
对一切正实数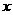 都成立?若存在,求出
都成立?若存在,求出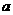 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
15.甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润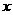 (元)与年产量
(元)与年产量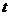 (吨)满足函数关系
(吨)满足函数关系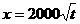 .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方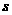 元(以下称
元(以下称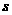 为赔付价格).
为赔付价格).
(1)将乙方的年利润 (元)表示为年产量
(元)表示为年产量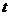 (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额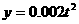 (元),在乙方按照获得最大利润的产量进行生产的前提下,w*w^w.k&s#5@甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,w*w^w.k&s#5@甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格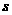 是多少?
是多少?
14.已知以点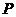 为圆心的圆经过点
为圆心的圆经过点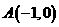 和
和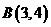 ,线段
,线段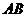 的垂直平分线交圆
的垂直平分线交圆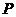
于点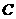 和
和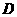 ,且
,且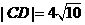 .
.
(1)求直线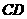 的方程;
⑵求圆
的方程;
⑵求圆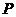 的方程;
的方程;
⑶设点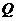 在圆
在圆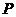 上w*w^w.k&s#5@,试问使△
上w*w^w.k&s#5@,试问使△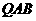 的面积等于8的点
的面积等于8的点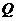 共有几个?证明你的结论.
共有几个?证明你的结论.
13.如图四边形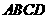 是菱形,
是菱形,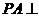 平面
平面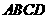 ,
,
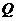 为
为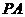 的中点. 求证:
的中点. 求证:
⑴ 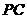 ∥平面
∥平面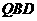 ;⑵ 平面
;⑵ 平面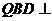 平面
平面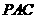 .
.
10.已知函数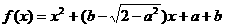 是偶函数,则此函数图象与
是偶函数,则此函数图象与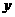 轴交点的纵坐标的最大值是
.
轴交点的纵坐标的最大值是
.
*11.已知点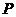 在直线
在直线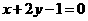 上,点
上,点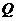 在直线
在直线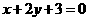 上,
上,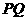 中点为
中点为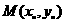 ,且
,且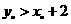 ,则
,则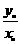 的取值范围为
.
的取值范围为
.
 *12.已知平面上的向量
*12.已知平面上的向量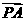 、
、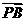 满足
满足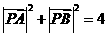 ,
,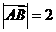 ,
,
设向量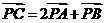 ,则
,则 的最小值是
.
的最小值是
.
9.设直线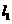 :
: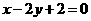 的倾斜角为
的倾斜角为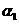 ,直线
,直线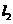 :
: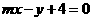 的倾斜角为
的倾斜角为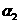 ,且
,且 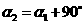 ,则w*w^w.k&s#5@
,则w*w^w.k&s#5@  的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com