
题目列表(包括答案和解析)
6.空间四边形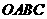 中,
中,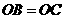 ,
,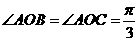 ,则
,则 <
<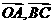 >的值是( )
>的值是( )
A.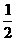 B.
B.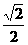 C.-
C.-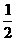 D.
D.
5.若A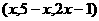 ,B
,B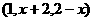 ,当
,当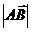 取最小值时,
取最小值时,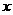 的值等于( )
的值等于( )
A.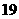 B.
B.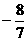 C.
C.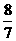 D.
D.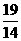
4.若A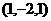 ,B
,B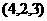 ,C
,C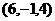 ,则△ABC的形状是( )
,则△ABC的形状是( )
A.不等边锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
3.若向量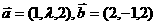 ,且
,且 与
与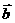 的夹角余弦为
的夹角余弦为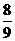 ,则
,则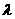 等于( )
等于( )
A.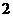 B.
B.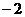 C.
C.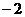 或
或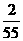 D.
D.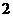 或
或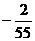
2.已知点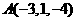 ,则点
,则点 关于
关于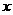 轴对称的点的坐标为( )
轴对称的点的坐标为( )
A.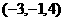 B.
B.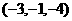 C.
C.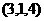 D.
D.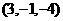
1.下列各组向量中不平行的是( )
A.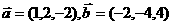 B.
B.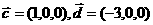
C.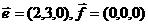 D.
D.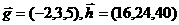
解法一:(1)
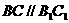 ,
,

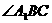 就是异面直线
就是异面直线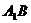 与
与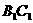 所成的角,
所成的角,
即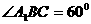 ,……(2分)
,……(2分)
连接 ,又
,又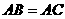 ,则
,则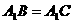

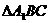 为等边三角形,……………………………4分
为等边三角形,……………………………4分
由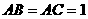 ,
,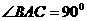
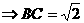 ,
,

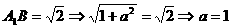 ;………6分
;………6分
(2)取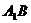 的中点
的中点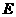 ,连接
,连接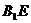 ,过
,过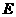 作
作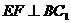 于
于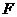 ,连接
,连接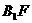 ,
,
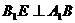 ,
,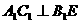
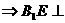 平面
平面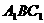
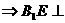
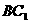 ………………8分
………………8分
又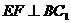 ,所以
,所以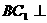 平面
平面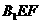 ,即
,即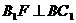 ,
,
所以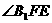 就是平面
就是平面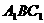 与平面
与平面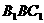 所成的锐二面角的平面角。…………10分
所成的锐二面角的平面角。…………10分
在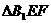 中,
中,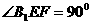 ,
,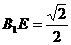 ,
,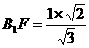 ,
,

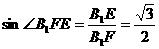
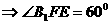 ,…………………………13分
,…………………………13分
因此平面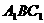 与平面
与平面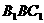 所成的锐二面角的大小为
所成的锐二面角的大小为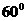 。…………14分
。…………14分
说明:取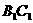 的中点
的中点 ,连接
,连接 ,…………同样给分(也给10分)
,…………同样给分(也给10分)
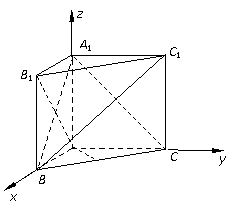
解法二:(1)建立如图坐标系,于是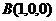 ,
,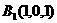 ,
,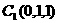 ,
,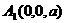 (
(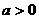 )
)
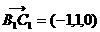 ,
,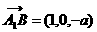 ,
,
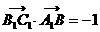 …………3分
…………3分
由于异面直线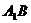 与
与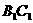 所成的角
所成的角 ,
,
 所以
所以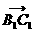 与
与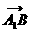 的夹角为
的夹角为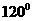
即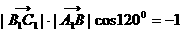
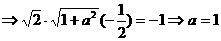 ………6分
………6分
(2)设向量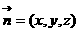 且
且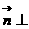 平面
平面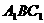
于是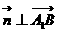 且
且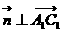 ,即
,即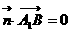 且
且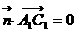 ,
,
又 ,
,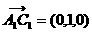 ,所以
,所以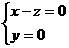 ,不妨设
,不妨设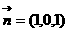 ……8分
……8分
 同理得
同理得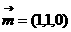 ,使
,使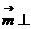 平面
平面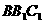 ,(10分)
,(10分)
设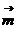 与
与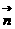 的夹角为
的夹角为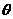 ,所以依
,所以依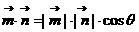 ,
,
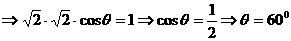 ,………………12分
,………………12分
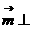 平面
平面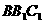 ,
,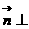 平面
平面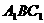 ,
,
因此平面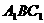 与平面
与平面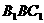 所成的锐二面角的大小为
所成的锐二面角的大小为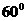 。…………14分
。…………14分
说明:或者取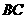 的中点
的中点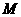 ,连接
,连接 ,于是
,于是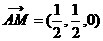 显然
显然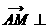 平面
平面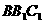
2. 解法一:(Ⅰ)取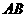 中点
中点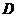 ,连结
,连结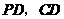 .
.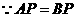 ,
,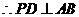 .
.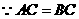 ,
,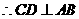 .
.
 ,
, 平面
平面 .
.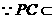 平面
平面 ,
,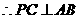 .
.
(Ⅱ)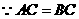 ,
,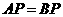 ,
,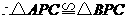 .又
.又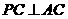 ,
,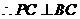 .
.
又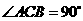 ,即
,即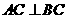 ,且
,且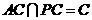 ,
,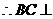 平面
平面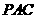 .取
.取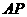 中点
中点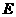 .连结
.连结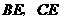 .
.
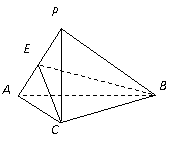
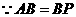 ,
,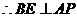 .
.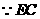 是
是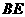 在平面
在平面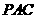 内的射影,
内的射影,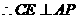 .
.
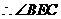 是二面角
是二面角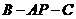 的平面角.在
的平面角.在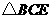 中,
中,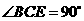 ,
,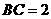 ,
,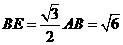 ,
,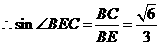 .
.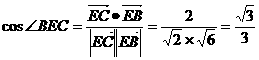
(Ⅲ)由(Ⅰ)知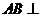 平面
平面 ,
, 平面
平面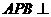 平面
平面 .过
.过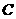 作
作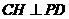 ,垂足为
,垂足为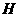 .
.
 平面
平面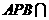 平面
平面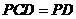 ,
,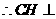 平面
平面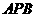 .
. 的长即为点
的长即为点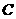 到平面
到平面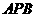 的距离.
的距离.
由(Ⅰ)知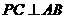 ,又
,又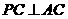 ,且
,且 ,
,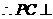 平面
平面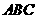 .
.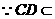 平面
平面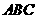 ,
,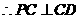 .在
.在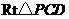 中,
中,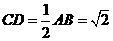 ,
,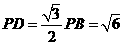 ,
,
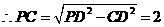 .
.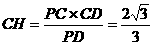 .
.
 点
点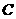 到平面
到平面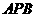 的距离为
的距离为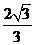 .
.
网解法二:(Ⅰ)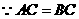 ,
,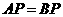 ,
,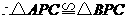 .又
.又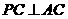 ,
,

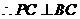 .
.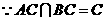 ,
,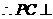 平面
平面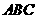 .
.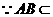 平面
平面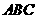 ,
,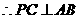 .
.
(Ⅱ)如图,以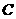 为原点建立空间直角坐标系
为原点建立空间直角坐标系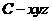 .则
.则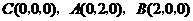 .
.
设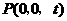 .
.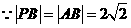 ,
,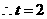 ,
,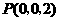 .取
.取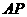 中点
中点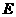 ,连结
,连结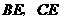 .
.
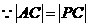 ,
,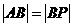 ,
,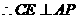 ,
,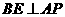 .
.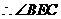 是二面角
是二面角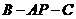 的平面角.
的平面角.
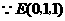 ,
,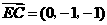 ,
,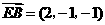 ,
,
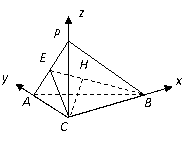
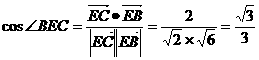 .
.
(Ⅲ)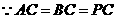 ,
,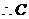 在平面
在平面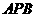 内的射影为正
内的射影为正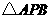 的中心
的中心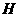 ,且
,且 的长为点
的长为点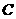 到平面
到平面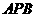 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系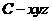 .
.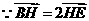 ,
, 点
点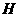 的坐标为
的坐标为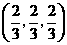 .
.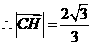 .
.  点
点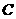 到平面
到平面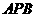 的距离为
的距离为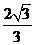 .
.
5、 [解析]此类求曲面上最短路程问题通常考虑侧面展开。侧面展开后得矩形 ,其中
,其中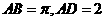 问题转化为在
问题转化为在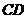 上找一点
上找一点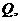 使
使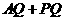 最短作
最短作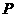 关于
关于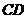 的对称点
的对称点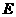 ,连接
,连接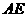 ,令
,令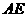 与
与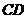 交于点
交于点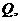 则得
则得 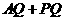 的最小值为
的最小值为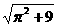
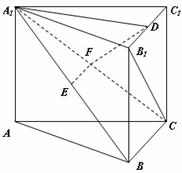 [答案]
[答案]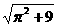
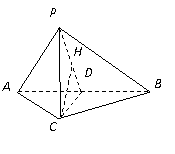
4、[解析]本题是立体几何中的最值问题,建立数学模型,用函数解决是一种重要方法。过A作AH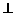 BP于H,连CH,
BP于H,连CH,
∴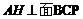 .
.
 ∴
∴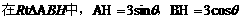 .
.
在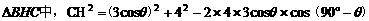 ,
,
 ∴在
∴在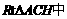 ,
,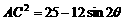 ,∴
,∴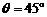 时,AC长最小;
时,AC长最小;
[答案]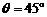
3、[解析] 三视图是新增考点,根据三张图的关系,可知几何体是正方体的一部分,是一个四棱锥。本题也可改编为求该几何体的外接球的表面积,则必须补全为正方体,增加了难度。
[答案]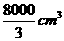
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com