
题目列表(包括答案和解析)
4、直线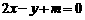 与圆
与圆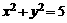 交于A、B,
交于A、B, 为坐标原点,若
为坐标原点,若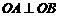 ,则
,则 的值为
的值为
(A)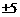 (B)
(B)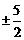 (C)
(C)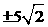 (D)
(D)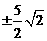
3、“ 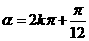
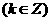 ”是“
”是“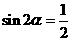 ”的 (
)
”的 (
)
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2、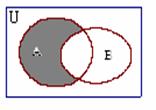 设全集
设全集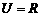 ,
,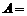
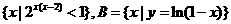 ,则右图中阴
,则右图中阴
影部分表示的集合为
A.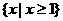 B.
B.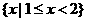 C.
C.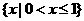 D.
D.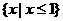
1、复数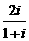 等于
等于
(A)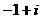 (B)
(B)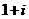 (C)
(C)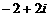 (D)
(D)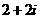
21. (14分) (2009广雅中学 节选)
节选)
已知数列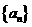 满足
满足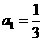 ,
,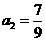 ,
,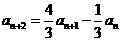
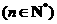 .
.
⑴求数列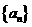 的通项公式;
的通项公式;
⑵求数列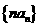 的前
的前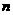 项和
项和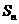 ;
;
[解析]⑴方法一:由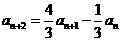 ,得
,得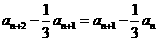 ,
,
∴数列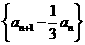 是常数列,
是常数列, ,
,
即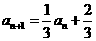 ,得
,得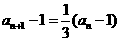 .
.
∴数列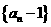 是首项为
是首项为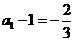 ,公比为
,公比为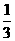 的等比数列,
的等比数列,
∴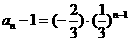 ,故数列
,故数列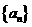 的通项公式为
的通项公式为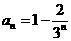 . …………7分
. …………7分
方法二:由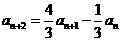 ,得
,得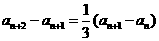 ,
,
∴数列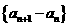 是首项为
是首项为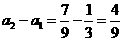 ,公比为
,公比为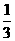 的等比数列,
的等比数列,
∴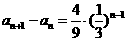 .
.
∴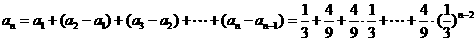
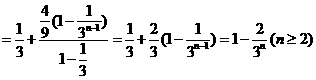 (*)
(*)
当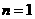 时,
时,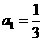 也适合(*),故数列
也适合(*),故数列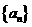 的通项公式为
的通项公式为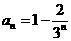 . …………7分
. …………7分
方法三:由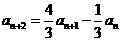 ,得
,得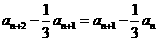 ,
,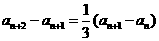 .
.
∴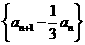 是常数列,
是常数列,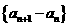 是首项为
是首项为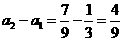 ,公比为
,公比为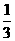 的等比数列.
的等比数列.
∴ ,且
,且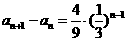 .
.
由上式联立消去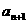 ,解得:
,解得: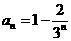 为数列
为数列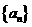 的通项公式.
………7分
的通项公式.
………7分
⑵解: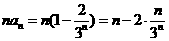 .
.
设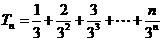 ,
① 则
,
① 则
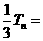
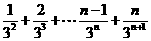 . ②
. ②
①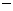 ②得:
②得: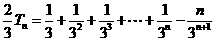
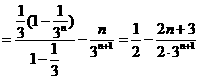 ,
,
∴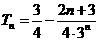 .
.
故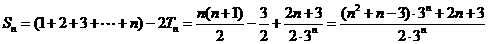 .……14分
.……14分
20. (14分)(2009年金山中学)
数列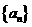 首项
首项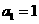 ,前
,前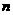 项和
项和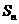 与
与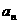 之间满足
之间满足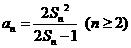 .
.
⑴求证:数列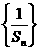 是等差数列;
是等差数列;
⑵求数列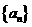 的通项公式;
的通项公式;
⑶设存在正数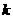 ,使
,使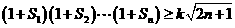 对
对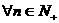 都成立,求
都成立,求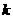 的最大值.
的最大值.
[解析]⑴因为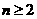 时,
时,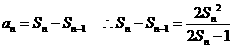 得
得
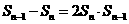
由题意 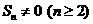
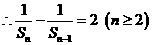
又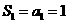
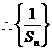 是以
是以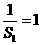 为首项,
为首项,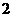 为公差的等差数列. (4分)
为公差的等差数列. (4分)
⑵由⑴有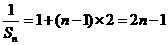
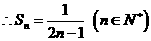
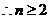 时,
时,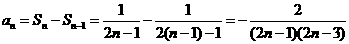
又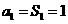
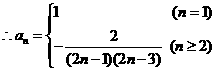 (8分)
(8分)
⑶ 设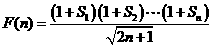
则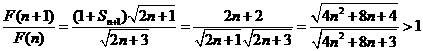
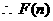 在
在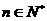 上递增 故使
上递增 故使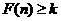 恒成立,只需
恒成立,只需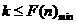 .
.
又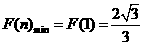 又
又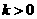
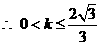 ,所以,
,所以,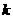 的最大值是
的最大值是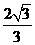 .(14分)
.(14分)
19.(13分)(2009广雅中学)已知等差数列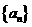 中,
中,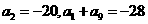 .
.
⑴求数列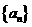 的通项公式;
的通项公式;
⑵若数列 满足
满足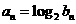 ,设
,设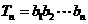 ,且
,且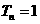 ,求
,求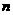 的值.
的值.
[解析]解:⑴设数列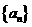 的公差为
的公差为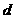 ,则
,则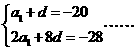 2分,解得
2分,解得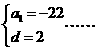 4分
4分
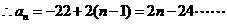 6分
6分
⑵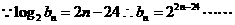 8分
8分
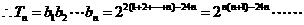 10分
10分
令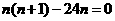 ,得
,得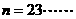 12分
12分
∴当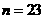 时,
时,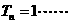 13分
13分
18. (14分)已知:公差不为零的等差数列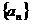 中,
中,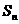 是其前
是其前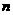 项和,且
项和,且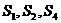 成等比数列.
成等比数列.
⑴求数列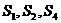 的公比
的公比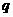 ;
;
⑵若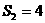 ,求等差数列
,求等差数列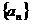 的通项公式.
的通项公式.
[解析]⑴设等差数列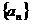 的公差为
的公差为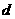 ,则
,则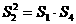 ,即
,即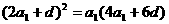 (2分)
(2分)

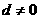 ,
,
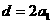 ,(5分)
,(5分) 
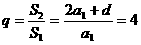 (7分)
(7分)
⑵由⑴知,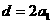 ,
①
,
①
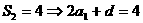 ② (9分)
② (9分)
由①②解得,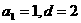 ,
,
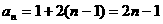 .
(14分)
.
(14分)
17. (12分)已知等比数列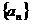 各项为正数,
各项为正数,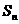 是其前
是其前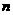 项和,且
项和,且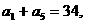
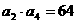 .
.
求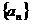 的公比
的公比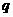 及
及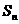 .
.
[解析] 数列
数列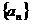 是等比数列,
是等比数列,
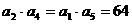 ,
(2分)
,
(2分)
又
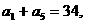

 或
或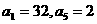 ,
(4分)
,
(4分)
由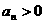 ,当
,当 时,
时,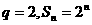 ,
(8分)
,
(8分)
当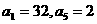 时,
时,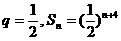 (12分)
(12分)
16. (13分)已知等差数列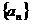 中,
中,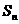 是其前
是其前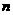 项和,
项和,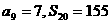 ,求:
,求: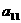 及
及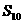 .
.
[解析]设等差数列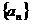 的公差为
的公差为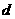 ,则
,则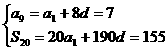 (4分)
(4分)
解得,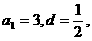 (8分)
(8分)

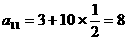 ,
,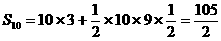 . (13分)
. (13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com