
题目列表(包括答案和解析)
8.(广东省六校2009届高三第二次联考试卷)一辆邮政车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,设该车从各站出发时邮政车内的邮袋数构成一个有穷数列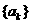 ,
,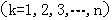
试求:(1)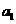
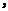
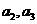
(2)邮政车从第k站出发时,车内共有邮袋数是多少个?
(3)求数列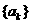 的前 k项和
的前 k项和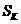 并证明:
并证明: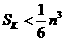
解: 满分14分
(1)由题意得: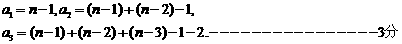
(2) 在第k站出发时,前面放上的邮袋共: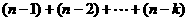 个
个
而从第二站起,每站放下的邮袋共:1+2+3+…+(k-1)个------------------5分
故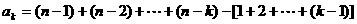
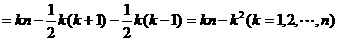
即邮政车从第k站出发时,车内共有邮袋数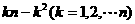 个-------------10分
个-------------10分
(3)
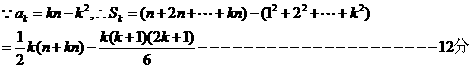
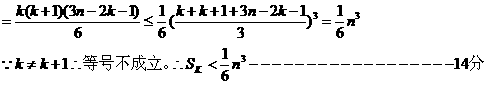
|

|
版权所有:()
版权所有:()
7. 已知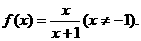
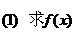 的单调区间;
的单调区间;
(2)若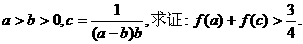
讲解: (1) 对 已 知 函 数 进 行 降 次 分 项 变 形 , 得 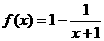 ,
,
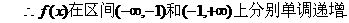
(2)首先证明任意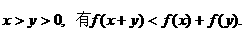
事实上,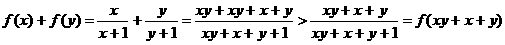
而 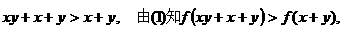
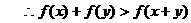

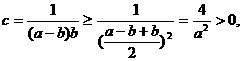
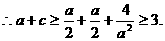
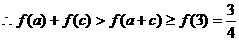 .
.
6.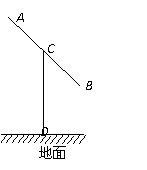 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求 至少长2.8m,
至少长2.8m,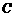 为
为 的中点,
的中点,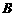 到
到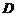 的距离比
的距离比 的长小0.5m,
的长小0.5m,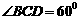 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?
解析:设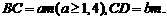
连结BD.
则在 中,
中,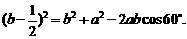
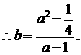
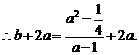
设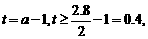
则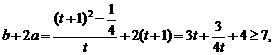
等号成立时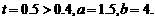
答:当 时,建造这个支架的成本最低.
时,建造这个支架的成本最低.
5. 某公司租地建仓库,每月土地占用费y1与车库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距车站10公里处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站多少公里处?
解析:由已知y1=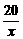 ;y2=0.8x(x为仓库与车站距离)费用之和y=y1+y2=0.8x+
;y2=0.8x(x为仓库与车站距离)费用之和y=y1+y2=0.8x+ 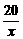 ≥2
≥2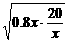 =8当且仅当0.8x=
=8当且仅当0.8x=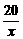 即x=5时“=”成立
即x=5时“=”成立
答:5公里处
综合拔高训练
4. 半径为4的球面上有A、B、C、D四点,且AB,AC,AD两两互相垂直,则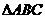 、
、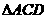 、
、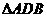 面积之和
面积之和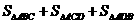 的最大值为 ( )C
的最大值为 ( )C
A.8 B.16 C.32 D.64
解析:由AB,AC,AD两两互相垂直,将之补成长方体知AB2+AC2+AD2=(2R)2=64.
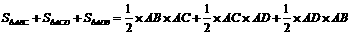
≤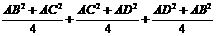 =
=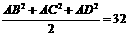 .
.
等号当且仅当 取得,所以
取得,所以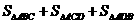 的最大值为32 ,选C.
的最大值为32 ,选C.
3. (广东省梅州、揭阳两市四校2008届高三第三次联考)设x,y均为正实数,且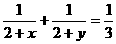 ,则xy的最小值为
,则xy的最小值为
解析:由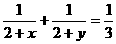 可化为xy =8+x+y,
可化为xy =8+x+y, x,y均为正实数
x,y均为正实数
 xy =8+x+y
xy =8+x+y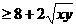 (当且仅当x=y等号成立)即xy-2
(当且仅当x=y等号成立)即xy-2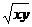 -8
-8
可解得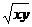
 ,即xy
,即xy 16故xy的最小值为16。
16故xy的最小值为16。
2. 设实数x,y满足,则x+y的取值范围是____.
解析:.答案为(-∞,-1]∪[1, +∞)_
1. 设x≠0,则函数在x=____时,y有最小值____.
解:.答案为: __±1__;3
7. (广东省潮州金中08-09学年高三上学期期中考试)某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为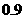 万元,年维修费用第一年是
万元,年维修费用第一年是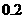 万元,以后逐年递增
万元,以后逐年递增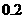 万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
万元。问这种汽车使用多少年时,它的年平均费用最小?最小值是多少?
解析:设使用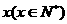 年的年平均费用为
年的年平均费用为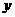 万元
则使用
万元
则使用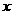 年的维修总费用为
年的维修总费用为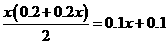 万元
万元
依题得
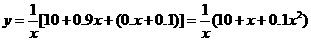
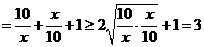 -
-
当且仅当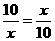 即
即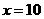 时取等号
时取等号
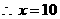 时
时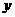 取得最小值3 万元
答:这种汽车使用10年时,它的年平均费用最小,最小值是3 万元.
取得最小值3 万元
答:这种汽车使用10年时,它的年平均费用最小,最小值是3 万元.
★ 抢 分 频 道 ★
基础巩固训练
6.已知函数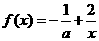 ,若
,若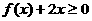 在(0,+
在(0,+ )上恒成立,求
)上恒成立,求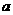 的取值范围。
的取值范围。
解析:因为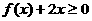 在(0,+
在(0,+ )上恒成立,即
)上恒成立,即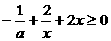
∴ 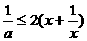 ∵
∵
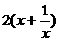 的最小值为4
∴
的最小值为4
∴ 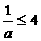
解得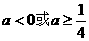
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com