
题目列表(包括答案和解析)
2. 若不等式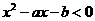 的解集为
的解集为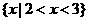 ,则不等式
,则不等式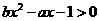 的解集为 __________.
的解集为 __________.
.解析:先由方程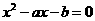 的两根为2和3求得
的两根为2和3求得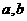 后再解不等式
后再解不等式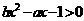 .得
.得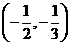
1. 不等式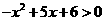 的解集是__________
的解集是__________
解析:将不等式转化成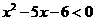 ,即
,即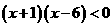 .]
.]
9.若不等式x2+ax+1³0对于一切xÎ(0,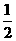 )成立,则a的取值范围是 ( )
)成立,则a的取值范围是 ( )
A.0
B.
–2 C.-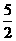 D.-3
D.-3
解析:设f(x)=x2+ax+1,则对称轴为x=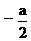 ,若
,若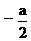 ³
³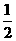 ,即a£-1时,则f(x)在(0,
,即a£-1时,则f(x)在(0,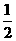 )上是减函数,应有f(
)上是减函数,应有f(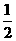 )³0Þ-
)³0Þ-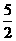 £x£-1
£x£-1
若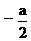 £0,即a³0时,则f(x)在(0,
£0,即a³0时,则f(x)在(0,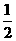 )上是增函数,应有f(0)=1>0恒成立,故a³0
)上是增函数,应有f(0)=1>0恒成立,故a³0
若0£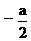 £
£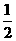 ,即-1£a£0,则应有f(
,即-1£a£0,则应有f(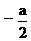 )=
)=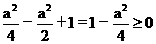 恒成立,故-1£a£0. 综上,有-
恒成立,故-1£a£0. 综上,有-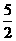 £a,故选C .
£a,故选C .
★ 抢 分 频 道 ★
基础巩固训练
8.不等式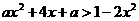 对一切
对一切 R恒成立,则实数a的取值范围是_______.
R恒成立,则实数a的取值范围是_______.
[解析]:不等式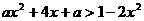 对一切
对一切 R恒成立,
R恒成立,
即 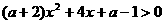 对一切
对一切 R恒成立
R恒成立
若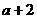 =0,显然不成立
=0,显然不成立
若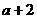
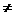 0,则
0,则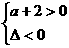 ∴
∴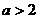
7.( 广东省深圳中学2008-2009学年度高三第一学段考试)解不等式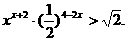
.解析: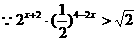
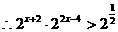
即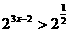 得
得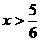 所以原不等式的解集为
所以原不等式的解集为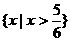
考点4 简单的恒成立问题
题型1:由二次函数的性质求参数的取值范围
例1.若关于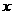 的不等式
的不等式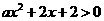 在
在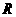 上恒成立,求实数
上恒成立,求实数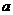 的取值范围.
的取值范围.
[解题思路]结合二次函数的图象求解
[解析]当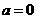 时,不等式
时,不等式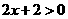 解集不为
解集不为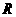 ,故
,故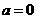 不满足题意;
不满足题意;
当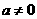 时,要使原不等式解集为
时,要使原不等式解集为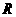 ,只需
,只需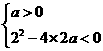 ,解得
,解得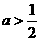
综上,所求实数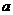 的取值范围为
的取值范围为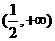
[名师指引]不等式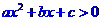 对一切
对一切 恒成立
恒成立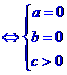 或
或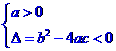
不等式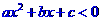 对任意
对任意 恒成立
恒成立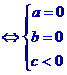 或
或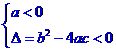
题型2.转化为二次函数的最值求参数的取值范围
[解题思路]先分离系数,再由二次函数最值确定取值范围.
[解析] (1)设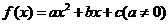 .由
.由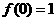 得
得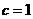 ,故
,故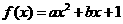 .
.
∵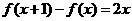 ∴
∴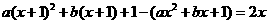
即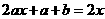 ,所以
,所以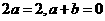 ,解得
,解得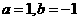 ∴
∴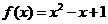
(2)由(1)知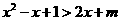 在
在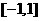 恒成立,即
恒成立,即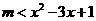 在
在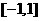 恒成立.
恒成立.
令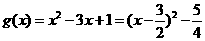 ,则
,则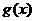 在
在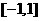 上单调递减.所以
上单调递减.所以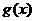 在
在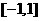 上的最大值为
上的最大值为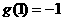 .所以
.所以 的取值范围是
的取值范围是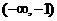 .
.
[名师指引]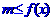 对一切
对一切 恒成立,则
恒成立,则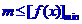 ;
;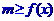 对一切
对一切 恒成立,则
恒成立,则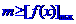 ;
;
[新题导练]
6. 解关于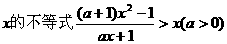
解:①若 ;
;
②若 ;
;
③若
5.若关于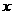 的不等式
的不等式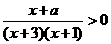 的解集是
的解集是 ,则
,则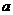 的值为_______
的值为_______
解析:原不等式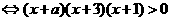 ,结合题意画出图可知
,结合题意画出图可知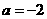 .
.
5.
考点3 分式不等式及高次不等式的解法
[例5] 解不等式: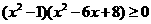
[解题思路]先分解因式,再标根求解
[解析]原不等式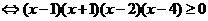 ,各因式根依次为-1,1,2,4,在数轴上标根如下:
,各因式根依次为-1,1,2,4,在数轴上标根如下:
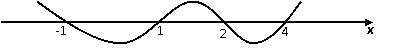
所以不等式的解集为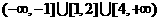 .
.
[名师指引]求解高次不等式或分式不等式一般用根轴法,要注意不等式的解集与不等式对应的方程的根的关系.
[新题导练]
4.解关于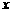 的不等式:
的不等式: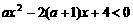
解析:
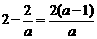
当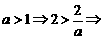
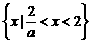 ;
;
当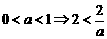
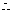
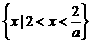 ,
,
当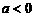
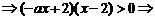
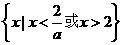
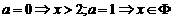
3.关于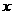 的不等式
的不等式 的解集为( )
的解集为( )
A.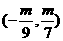 B.
B.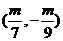 C.
C.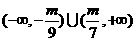 D.以上答案都不对
D.以上答案都不对
解析:原不等式可化为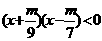 ,需对
,需对 分三种情况讨论,即不等式的解集与
分三种情况讨论,即不等式的解集与 有关.
有关.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com