
题目列表(包括答案和解析)
2.在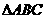 中,
中,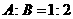 ,
,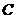 的平分线
的平分线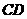 把三角形面积分成
把三角形面积分成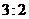 两部分,则
两部分,则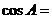 ( )
( )
A 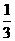 B
B
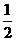 C
C
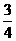 D
D

解析:∵ 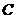 的平分线
的平分线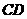 把三角形面积分成
把三角形面积分成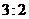 两部分, ∴
两部分, ∴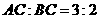 ,
,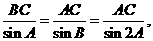 ∴
∴ 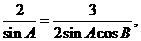 ∴
∴
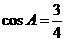 ]
]
1.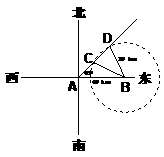 台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为( )
台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为( )
A.0.5小时 B.1小时 C.1.5小时 D.2小时
解析:设A地东北方向上点P到B的距离为30千米,AP=x,在△ABP中
PB2=AP2+AB2-2AP·AB·cosA,
即302=x2+402-2x·40cos450
化简得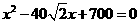
|x1-x2|2=(x1+x2)2-4x1x2=400,|x1-x2|=20,即CD=20
故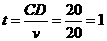 ]
]
8. 设三次函数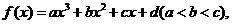 在
在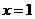 处取得极值,其图象在
处取得极值,其图象在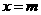 处的切线的斜率为
处的切线的斜率为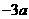 。求证:
。求证: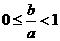 ;
;
解:(Ⅰ)方法一、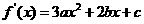 .由题设,得
.由题设,得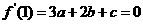 ①
①
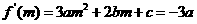 ②
②
∵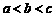 ,∴
,∴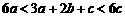 ,∴
,∴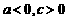 。
。
由①代入②得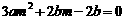 ,∴
,∴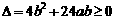 ,
,
得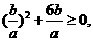 ∴
∴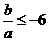 或
或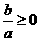 ③
③
将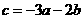 代入
代入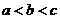 中,得
中,得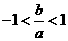 ④
④
由③、④得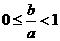 ;
;
方法二、同上可得: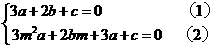 将(1)变为:
将(1)变为: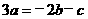 代入(2)可得:
代入(2)可得: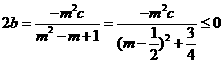 ,所以
,所以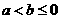 ,则
,则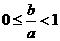
方法三:同上可得: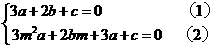 将(1)变为:
将(1)变为: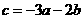 代入(2)可得:
代入(2)可得: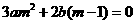 ,显然
,显然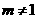 ,所以
,所以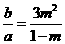
因为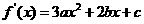 图象的开口向下,且有一根为x1=1
图象的开口向下,且有一根为x1=1
由韦达定理得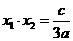 ,
,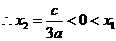
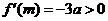 ,所以
,所以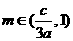 ,即
,即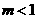 ,则
,则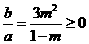 ,由
,由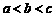 得:
得: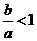
所以: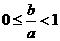
|

|
版权所有:()
版权所有:()
7.已知定义在正实数集上的函数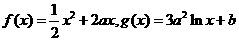 ,其中
,其中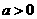 。设两曲线
。设两曲线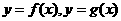 有公共点,且在公共点处的切线相同。
有公共点,且在公共点处的切线相同。
(1)若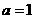 ,求
,求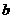 的值;
的值;
(2)用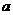 表示
表示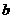 ,并求
,并求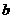 的最大值。
的最大值。
解:(1)设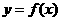 与
与 在公共点
在公共点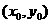 处的切线相同
处的切线相同
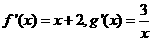
由题意知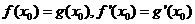 ,∴
,∴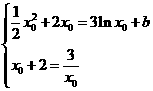
由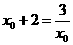 得,
得,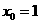 ,或
,或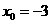 (舍去)
(舍去)
即有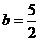
(2)设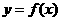 与
与 在公共点
在公共点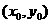 处的切线相同
处的切线相同
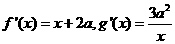
由题意知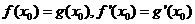 ,∴
,∴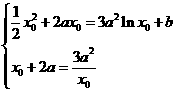
由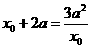 得,
得,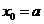 ,或
,或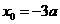 (舍去)
(舍去)
即有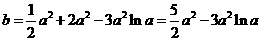
令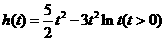 ,则
,则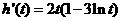 ,于是
,于是
当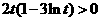 ,即
,即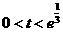 时,
时,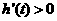 ;
;
当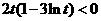 ,即
,即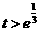 时,
时,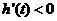
故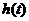 在
在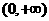 的最大值为
的最大值为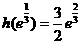 ,故
,故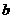 的最大值为
的最大值为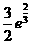
6. 对于三次函数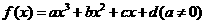 ,定义:设
,定义:设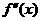 是函数
是函数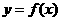 的导函数
的导函数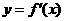 的导数,若
的导数,若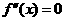 有实数解
有实数解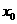 ,则称点
,则称点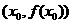 为函数
为函数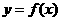 的“拐点”。现已知
的“拐点”。现已知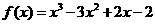 ,请解答下列问题:
,请解答下列问题:
(1)求函数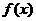 的“拐点”A的坐标;
的“拐点”A的坐标;
(2)求证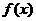 的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明).
[解析](1)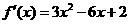 ,
,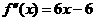 .令
.令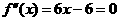 得
得
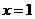 ,
, 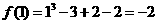 .
. 拐点
拐点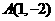
(2)设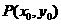 是
是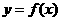 图象上任意一点,则
图象上任意一点,则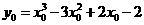 ,因为
,因为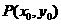 关于
关于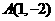 的对称点为
的对称点为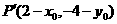 ,把
,把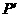 代入
代入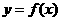 得
得
左边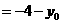
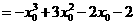 ,
,
右边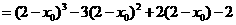
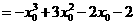
 右边=右边
右边=右边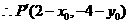 在
在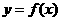 图象上
图象上
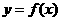 关于A对称
关于A对称
5.(湛江市实验中学2009届高三第四次月考)
已知函数 的图象都相切,且l与函数
的图象都相切,且l与函数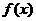 图象的切点的横坐标为1,求直线l的方程及a的值;
图象的切点的横坐标为1,求直线l的方程及a的值;
解由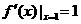 ,故直线l的斜率为1,切点为
,故直线l的斜率为1,切点为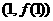
即(1,0) ∴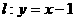 ① 又∵
① 又∵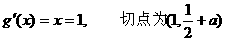
∴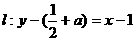 即
即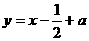 ②
②
比较①和②的系数得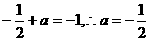
综合拔高训练
4.(广东省深圳市2008年高三年级第一次调研考试)已知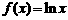 ,
,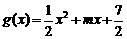 (
(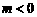 ),直线
),直线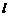 与函数
与函数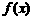 、
、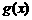 的图像都相切,且与函数
的图像都相切,且与函数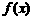 的图像的切点的横坐标为1.求直线
的图像的切点的横坐标为1.求直线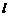 的方程及
的方程及 的值;
的值;
解:依题意知:直线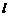 是函数
是函数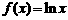 在点
在点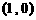 处的切线,故其斜率
处的切线,故其斜率
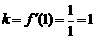 ,
,
所以直线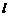 的方程为
的方程为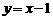 .
.
又因为直线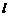 与
与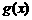 的图像相切,所以由
的图像相切,所以由
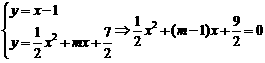 ,
,
得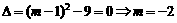 (
(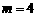 不合题意,舍去);
不合题意,舍去);
3. 已知直线x+2y-4=0与抛物线y2=4x相交于A、B两点,O是坐标原点,P是抛物线的弧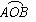 上求一点P,当△PAB面积最大时,P点坐标为
.
上求一点P,当△PAB面积最大时,P点坐标为
.
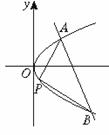
解析:|AB|为定值,△PAB面积最大,只要P到AB的距离最大,只要点P是抛物线的平行于AB的切线的切点,设P(x,y).由图可知,点P在x轴下方的图象上
∴y=-2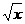 ,∴y′=-
,∴y′=-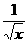 ,∵kAB=-
,∵kAB=-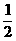 ,∴-
,∴-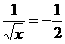
∴x=4,代入y2=4x(y<0)得y=-4. ∴P(4,-4)
2. (广东省2008届六校第二次联考) 在
在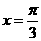 处的导数值是___________.
处的导数值是___________.
解析: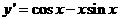 故填
故填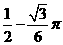
1. (广东省六校2009届高三第二次联考试卷)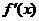 是
是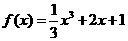 的导函数,则
的导函数,则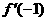 的值是 .
的值是 .
解析: 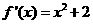 故
故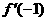 =3
=3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com