
题目列表(包括答案和解析)
4. (广东省惠州市2009届高三第二次调研考试)设变量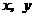 满足约束条件:
满足约束条件: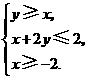 ,则
,则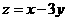 的最小值( )
的最小值( )
A.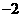 B.
B.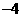 C.
C.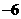 D.
D.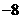
解析:画出可行域与目标函数线如下图可知,目标函数在点(-2,-2)取最小值-8.
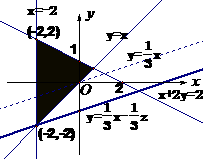 ∴选D.
∴选D.
3. 已知变量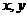 满足约束条件
满足约束条件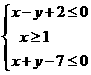 ,则
,则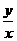 的取值范围是______.
的取值范围是______.
解析:由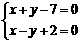 得
得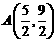 ∴
∴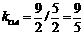 ;
;
由 得
得 ∴
∴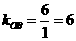
∵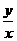 表示过可行域内一点
表示过可行域内一点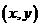 及原点的直线的斜率
及原点的直线的斜率
∴由约束条件画出可行域(如图),则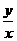 的取值范围为
的取值范围为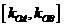 ,即
,即 ;
;
考点2 线性规划中求目标函数的最值问题
题型: 求目标函数的最值
例1. 设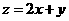 ,式中变量
,式中变量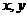 满足条件
满足条件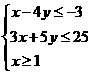 ,求
,求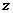 的最大值和最小值.
的最大值和最小值.
[解题思路]按解题步骤求解.
 [解析]作出可行域如图8-3-6所示,作直线
[解析]作出可行域如图8-3-6所示,作直线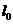 :
: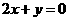 上,
上,
作一组平行于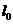 的直线
的直线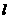 :
: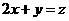 ,
,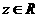 ,
,
可知:直线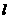 往右平移时,
往右平移时,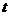 随之增大。
随之增大。
由图象可知,当直线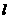 经过点
经过点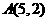 时,对应的
时,对应的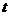 最大,
最大,
当直线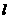 经过点
经过点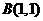 时,对应的
时,对应的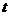 最小,
最小,
所以,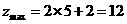 ,
,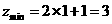 .
.
[名师指引]要注意到线性目标函数的最大(小)值往往是在边界处取到.
例2. 已知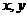 满足不等式组
满足不等式组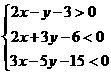 ,求使
,求使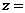
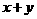 取最大值的整数
取最大值的整数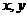 .
.
[解题思路]先作平面区域,再作一组平行线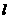 :
: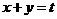 平行于
平行于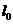 :
: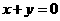
进一步寻找整点.
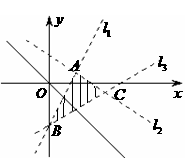 [解析]不等式组的解集为三直线
[解析]不等式组的解集为三直线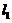 :
: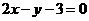 ,
,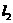 :
: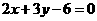 ,
,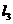 :
: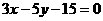 所围成的三角形内部(不含边界),设
所围成的三角形内部(不含边界),设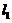 与
与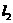 ,
,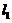 与
与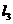 ,
,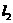 与
与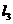 交点分别为
交点分别为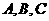 ,则
,则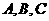 坐标分别为
坐标分别为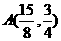 ,
,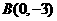 ,
,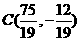 ,
,
作一组平行线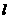 :
: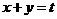 平行于
平行于 :
: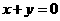 ,
,
当 往
往 右上方移动时,
右上方移动时,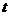 随之增大,
随之增大,
∴当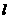 过
过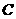 点时
点时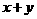 最大为
最大为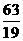 ,但不是整数解,
,但不是整数解,
又由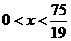 知
知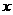 可取
可取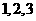 ,
,
当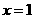 时,代入原不等式组得
时,代入原不等式组得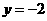 ,
∴
,
∴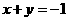 ;
;
当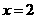 时,得
时,得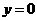 或
或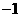 ,
∴
,
∴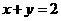 或
或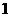 ;
;
当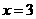 时,
时,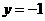 ,
∴
,
∴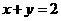 ,故
,故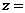
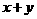 的最大整数解为
的最大整数解为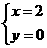 或
或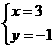 .
.
[名师指引]在平行域内找整点最优解,一般采用平移找解法,即打网格,描整点,平移直线,找出最优解
[新题导练]
2.如果直线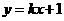 与圆
与圆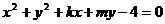 相交于
相交于 两点,且点
两点,且点 关于直线
关于直线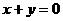 对称,则不等式组
对称,则不等式组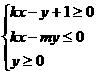 所表示的平面区域的面积为________.
所表示的平面区域的面积为________.
解析:因为M、N两点关于直线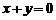 对称,所以直线
对称,所以直线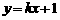 的斜率
的斜率 ,
,
而圆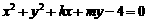 的圆心
的圆心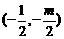 在直线
在直线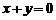 上,所以
上,所以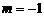 ,则不
,则不
等式组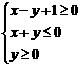 表示的平面区域就是一个斜边长为1的等腰直角三角形,面积为
表示的平面区域就是一个斜边长为1的等腰直角三角形,面积为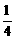 .
.
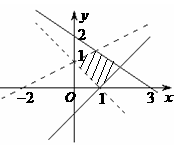
1. 图中阴影部分是下列不等式中( )表示的平面区域.
 A.
A.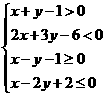 B.
B.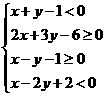
C.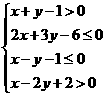 D.
D.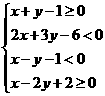
解析:用原点作检验.选C
8. 在一很大的湖岸边(可视湖岸为直线)停放着一只小船,由于缆绳突然断开,小船被风
刮跑,其方向与湖岸成15°角,速度为2.5km/h,同时岸边有一人,从同一地点开始追赶小
船,已知他在岸上跑的速度为4km/h,在水中游的速度为2km/h.问此人能否追上小船.若小
船速度改变,则小船能被人追上的最大速度是多少?
解析:设船速为v,显然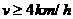 时人是不可能追上小船,当
时人是不可能追上小船,当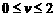 km/h时,人不必在岸上跑,而只要立即从同一地点直接下水就可以追上小船,因此只要考虑
km/h时,人不必在岸上跑,而只要立即从同一地点直接下水就可以追上小船,因此只要考虑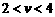 的情况,由于人在水中游的速度小于船的速度,人只有先沿湖岸跑一段路后再游水追赶,当人沿岸跑的轨迹和人游水的轨迹以及船在水中漂流的轨迹组成一个封闭的三角形时,人才能追上小船.设船速为v,人追上船所用时间为t,人在岸上跑的时间为
的情况,由于人在水中游的速度小于船的速度,人只有先沿湖岸跑一段路后再游水追赶,当人沿岸跑的轨迹和人游水的轨迹以及船在水中漂流的轨迹组成一个封闭的三角形时,人才能追上小船.设船速为v,人追上船所用时间为t,人在岸上跑的时间为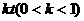 ,则人在水中游的时间为
,则人在水中游的时间为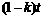 ,人要追上小船,则人船运动的路线满足如图所示的三角形.
,人要追上小船,则人船运动的路线满足如图所示的三角形.
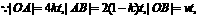 由余弦是理得
由余弦是理得
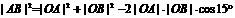 ,
,
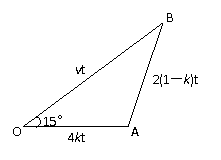 即
即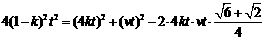 ,
,
整理得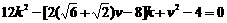 ,
,
要使上式在(0,1)范围内有实数解,
则有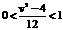 且
且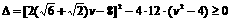 ,
,
解得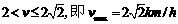 ,
,
故当船速在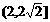 内时,人船运动路线可构成三角形,即人能追上小船,船能使人追上的最大速度为
内时,人船运动路线可构成三角形,即人能追上小船,船能使人追上的最大速度为 ,由此可见当船速为2.5km/h时人可以追上小船.
,由此可见当船速为2.5km/h时人可以追上小船.
|

|
版权所有:()
版权所有:()
7. 在正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上,在这种情况下,若要使AD最小,求AD∶AB的值
解 按题意,设折叠后A点落在边BC上改称P点,显然A、P两点关于折线DE对称,又设∠BAP=θ,∴∠DPA=θ,∠BDP=2θ,
再设AB=a,AD=x,∴DP=x 在△ABC中,
∠APB=180°-∠ABP-∠BAP=120°-θ,
由正弦定理知 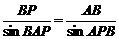 ∴BP=
∴BP=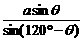
在△PBD中,
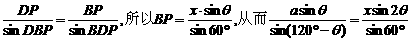 ,
,
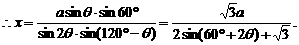
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,
∴当60°+2θ=90°,即θ=15°时,
sin(60°+2θ)=1,此时x取得最小值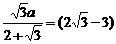 a,即AD最小,
a,即AD最小,
∴AD∶DB=2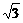 -3
-3
6.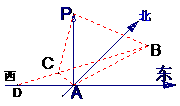 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为30°的B处,到11时10分又测得该船在岛北60°西、俯角为60°的C处。
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为30°的B处,到11时10分又测得该船在岛北60°西、俯角为60°的C处。
(1)求船的航行速度是每小时多少千米;
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
解 (1)在Rt△PAB中,∠APB=60° PA=1,∴AB=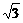 (千米)
(千米)
在Rt△PAC中,∠APC=30°,∴AC=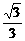 (千米)
(千米)
在△ACB中,∠CAB=30°+60°=90°
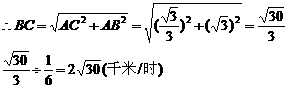
(2)∠DAC=90°-60°=30°
sinDCA=sin(180°-∠ACB)=sinACB=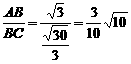
sinCDA=sin(∠ACB-30°)=sinACB·cos30°-cosACB·sin30°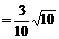
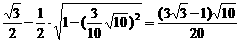
在△ACD中,据正弦定理得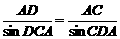 ,
,
∴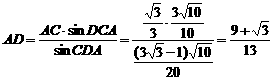
答 此时船距岛A为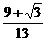 千米
千米
5.(08年韶关市二模) 某市电力部门在今年的抗雪救灾的某项重建工程中,需要在 、
、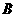 两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离. 现测量人员在相距
两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离. 现测量人员在相距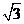
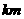 的
的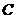 、
、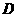 两地(假设
两地(假设 、
、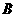 、
、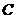 、
、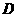 在同一平面上),测得∠
在同一平面上),测得∠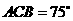 ,
,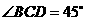 ,
,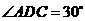 ,
,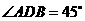 (如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是
(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是 、
、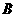 距离的
距离的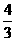 倍,问施工单位至少应该准备多长的电线?
倍,问施工单位至少应该准备多长的电线?
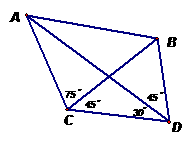
解:在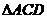 中,由已知可得,
中,由已知可得,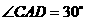
所以,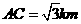 ………
………
在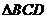 中,由已知可得,
中,由已知可得,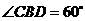
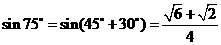
由正弦定理,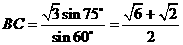
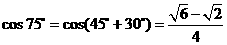
在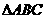 中,由余弦定理
中,由余弦定理
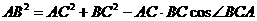
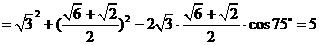
所以,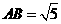 施工单位应该准备电线长
施工单位应该准备电线长 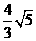 .
.
答:施工单位应该准备电线长
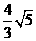
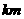 .
.
综合拔高训练
4.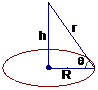 如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·
如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·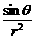 ,其中 k是一个和灯光强度有关的常数,那么电灯悬挂的高度h=
,才能使桌子边缘处最亮.
,其中 k是一个和灯光强度有关的常数,那么电灯悬挂的高度h=
,才能使桌子边缘处最亮.
解 R=rcosθ,由此得 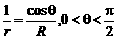 ,
,
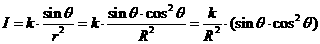
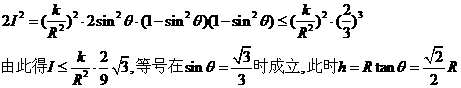
3.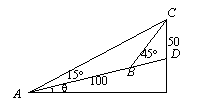 如图,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度q,则cosq= .
如图,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度q,则cosq= .
[解析] 在△ABC中,AB = 100m , ÐCAB = 15°, ÐACB = 45°-15° = 30°
由正弦定理: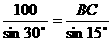
∴BC = 200sin15°
在△DBC中,CD = 50m , ÐCBD = 45°, ÐCDB = 90° + q
由正弦定理: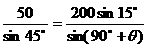 Þcosq =
Þcosq =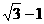 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com