
题目列表(包括答案和解析)
5.(上海卷理12)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去 ,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
解析:翻折后的几何体为底面边长为4,侧棱长为 的正三棱锥,
的正三棱锥,
高为 所以该四面体的体积为
所以该四面体的体积为
4.(全国Ⅱ卷理16文16)已知球 的半径为4,圆
的半径为4,圆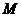 与圆
与圆 为该球的两个小圆,
为该球的两个小圆,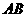 为圆
为圆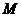 与圆
与圆 的公共弦,
的公共弦, .若
.若 ,则两圆圆心的距离
,则两圆圆心的距离
 .
.
[答案]3
[命题意图]本试题主要考查球的截面圆的性质,解三角形问题.
 [解析]设E为AB的中点,则O,E,M,N四点共面,如图,∵
[解析]设E为AB的中点,则O,E,M,N四点共面,如图,∵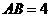 ,所以
,所以 ,∴
,∴ ,由球的截面性质,有
,由球的截面性质,有 ,∵
,∵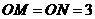 ,所以
,所以 与
与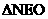 全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
3.(江西卷文16)长方体 的顶点均在同一个球面上,
的顶点均在同一个球面上, ,
, ,则
,则 ,
, 两点间的球面距离为
.
两点间的球面距离为
.
[答案]
[解析]考查球面距离,可先利用长方体三边长求出球半径,在三角形中求出球心角,再利用球面距离公式得出答案
2. (江西卷理16)如图,在三棱锥
(江西卷理16)如图,在三棱锥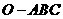 中,三条棱
中,三条棱 ,
,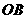 ,
, 两两垂直,且
两两垂直,且 >
>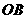 >
> ,分别经过三条棱
,分别经过三条棱 ,
,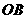 ,
, 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为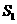 ,
, ,
, ,则
,则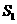 ,
, ,
, 的大小关系为
。
的大小关系为
。
[答案] 
[解析]考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得 。
。
1.(湖北卷理13文14)圆柱形容器内部盛有高度为8 cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.
[答案]4
[解析]设球半径为r,则由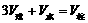 可得
可得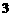
 ,解得r=4.
,解得r=4.
12.(四川卷理11文12)半径为 的球
的球 的直径
的直径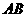 垂直于平面
垂直于平面 ,垂足为
,垂足为 ,
,
 是平面
是平面 内边长为
内边长为 的正三角形,线段
的正三角形,线段 、
、 分别
分别
与球面交于点M,N,那么M、N两点间的球面距离是
(A) (B)
(B)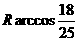 (C)
(C)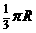 (D)
(D)
解析:由已知,AB=2R,BC=R,故tan∠BAC= cos∠BAC=
cos∠BAC=
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC= ,同理AN=
,同理AN= ,且MN∥CD
,且MN∥CD
而AC= R,CD=R
R,CD=R
故MN:CD=AN:AC
Þ MN= ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=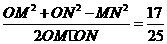
 所以M、N两点间的球面距离是
所以M、N两点间的球面距离是
答案:A
10.(全国Ⅰ新卷文7)设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为
(A)3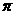 a2
(B)6
a2
(B)6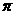 a2 (C)12
a2 (C)12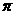 a2 (D) 24
a2 (D) 24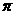 a2
a2
[答案]B
解析:根据题意球的半径 满足
满足 ,所以
,所以 .
.
11(全国Ⅱ卷理9)已知正四棱锥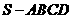 中,
中, ,那么当该棱锥的体积最大时,它的高为
,那么当该棱锥的体积最大时,它的高为
(A)1
(B) (C)2
(D)3
(C)2
(D)3
[答案]C
[命题意图]本试题主要考察椎体的体积,考察告辞函数的最值问题.
[解析]设底面边长为a,则高 所以体积
所以体积 ,
,
设 ,则
,则 ,当y取最值时,
,当y取最值时, ,解得a=0或a=4时,体积最大,此时
,解得a=0或a=4时,体积最大,此时 ,故选C.
,故选C.
9.(全国Ⅰ新卷理10)设三棱柱的侧棱垂直于底面,所有棱长都为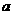 ,顶点都在一个球面上,则该球的表面积为
,顶点都在一个球面上,则该球的表面积为
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
 [答案]B
[答案]B
解析:如图,P为三棱柱底面中心,O为球心,易知
 ,所以球的半径
,所以球的半径 满足:
满足:
 ,故
,故 .
.
8.(全国Ⅰ卷理12文12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 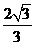 (B)
(B) (C)
(C)  (D)
(D) 
[答案].B[命题意图]本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
[解析]过CD作平面PCD,使AB⊥平面PCD,交AB与P,设点P到CD的距离为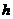 ,则有
,则有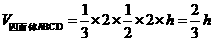 ,当直径通过AB与CD的中点时,
,当直径通过AB与CD的中点时,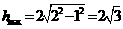 ,故
,故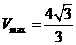 .
.
7. (辽宁卷文11)已知
(辽宁卷文11)已知 是球
是球 表面上的点,
表面上的点, ,
, ,
,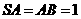 ,
, ,则球
,则球 的表面积等于
的表面积等于
(A)4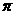 (B)3
(B)3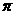 (C)2
(C)2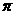 (D)
(D)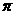
解析:选A.由已知,球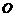 的直径为
的直径为 ,
, 表面积为
表面积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com