
题目列表(包括答案和解析)
(三)例题分析:
例1.求下列函数的定义域:
(1)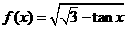 ;(2)
;(2) ;(3)
;(3)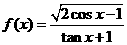 .
.
解:(1)由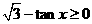 ,得
,得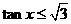 ,∴
,∴ .
.
∴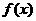 的定义域为
的定义域为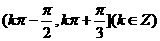 .
.
(2)∵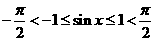 ,∴
,∴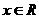 .即
.即 的定义域为
的定义域为 .
.
(3)由已知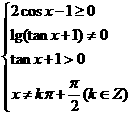 ,得
,得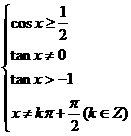 ,
,
∴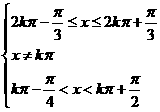
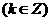 ,
,
∴原函数的定义域为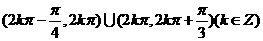 .
.
例2.求下列函数的值域:(1)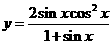 ;(2)
;(2)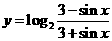 ;
;
(3)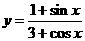 .
.
解:由题意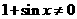 ,
,
∴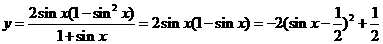 ,
,
∵ ,∴
,∴ 时,
时,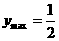 ,但
,但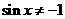 ,∴
,∴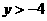 ,
,
∴原函数的值域为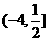 .
.
(2)∵ ,又∵
,又∵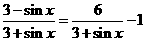 ,∴
,∴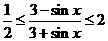 ,∴
,∴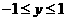 ,
,
∴函数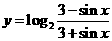 的值域为
的值域为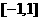 .
.
(3)由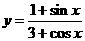 得
得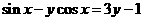 ,∴
,∴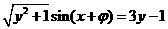 ,
,
这里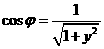 ,
,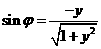 .
.
∵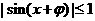 ,∴
,∴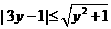 .解得
.解得 ,
,
∴原函数的值域为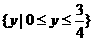 .
.
例3.求下列函数的周期:
(1)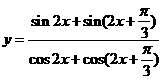 ;(2)
;(2)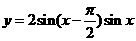 ;(3)
;(3)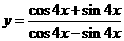 .
.
解:(1)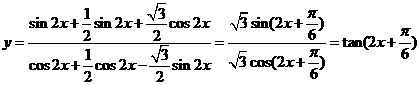 ,∴周期
,∴周期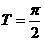 .
.
(2) ,故周期
,故周期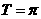 .
.
(3)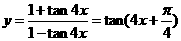 ,故周期
,故周期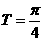 .
.
例4.若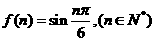 ,试求:
,试求: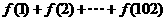 的值.
的值.
解:∵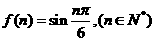 的周期为12,
的周期为12,
而 ,
,
∴ ,
,
∴原式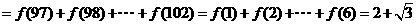 .
.
(二)主要方法:
1.求三角函数的定义域实质就是解三角不等式(组).一般可用三角函数的图象或三角函数线确定三角不等式的解.列三角不等式,既要考虑分式的分母不能为零;偶次方根被开方数大于等于零;对数的真数大于零及底数大于零且不等于1,又要考虑三角函数本身的定义域;
2.求三角函数的值域的常用方法:①化为求代数函数的值域;②化为求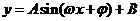 的值域;③化为关于
的值域;③化为关于 (或
(或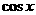 )的二次函数式;
)的二次函数式;
3.三角函数的周期问题一般将函数式化为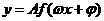 (其中
(其中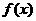 为三角函数,
为三角函数,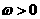 ).
).
(一)主要知识:
三角函数的定义域、值域及周期如下表:
|
函数 |
定义域 |
值域 |
周期 |
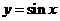 |
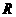 |
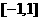 |
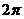 |
 |
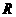 |
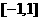 |
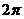 |
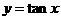 |
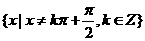 |
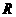 |
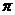 |
|

|
版权所有:()
版权所有:()
(四)巩固练习:
1.①函数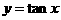 在它的定义域内是增函数;②若
在它的定义域内是增函数;②若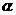 、
、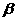 是第一象限角,且
是第一象限角,且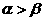 ,则
,则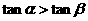 ;③函数
;③函数 一定是奇函数;④函数
一定是奇函数;④函数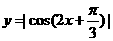 的最小正周期为
的最小正周期为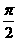 .上列四个命题中,正确的命题是(
.上列四个命题中,正确的命题是( 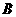 )
)
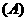 ①
①
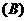 ④
④  ①、②
①、②
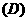 ②、③
②、③
2.若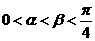 ,
,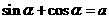 ,
,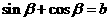 ,则 (
,则 (  )
)
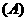

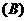
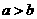

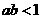
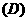
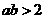
3.函数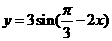 的单调递减区间是
的单调递减区间是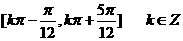 .
.
(三)例题分析:
例1.判断下列函数的奇偶性:(1)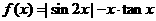 ;(2)
;(2) .
.
解:(1)∵ 的定义域为
的定义域为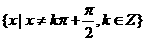 ,∴定义域关于原点对称,
,∴定义域关于原点对称,
又∵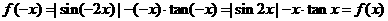 ,∴
,∴ 为偶函数.
为偶函数.
(2)∵ 的定义域为
的定义域为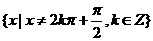 不关于原点对称,∴
不关于原点对称,∴ 为非奇非偶函数.
为非奇非偶函数.
例2.比较下列各组中两个值的大小:
(1)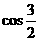 ,
,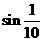 ,
,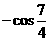 ;(2)
;(2)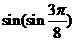 ,
,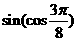 .
.
解:(1)∵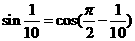 ,
,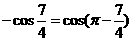 ,
,
又∵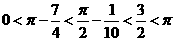 及
及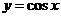 在
在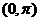 内是减函数,
内是减函数,
∴可得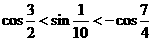 .
.
(2)∵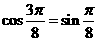 ,∴
,∴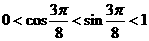 ,而
,而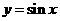 在
在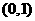 上递增,
上递增,
∴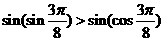 .
.
例3.设定义域为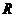 的奇函数
的奇函数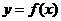 是减函数,若当
是减函数,若当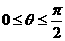 时,
时,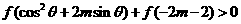 ,求
,求 的值.
的值.
解:∵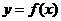 是奇函数,∴
是奇函数,∴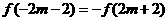 ,原不等式可化为
,原不等式可化为
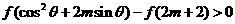 ,即
,即 .
.
∵ 是减函数,∴
是减函数,∴ ,
,
即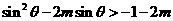 ,
,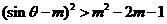 .
.
∵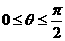 ,∴
,∴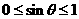 .
.
当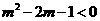 即
即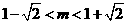 时,
时,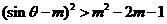 成立;
成立;
当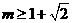 时,
时, ,即
,即 成立;
成立;
当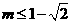 时,
时,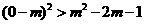 ,即
,即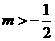 .
.
综上所述, 的取值范围是
的取值范围是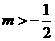 .
.
例4.《高考 计划》考点31,智能训练13:已知函数
计划》考点31,智能训练13:已知函数
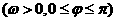 是
是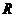 上的偶函数,其图象关于点
上的偶函数,其图象关于点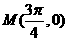 对称,且在区间
对称,且在区间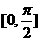 上是单调函数,求
上是单调函数,求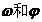 的值.
的值.
解:由 是
是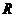 上的偶函数,得
上的偶函数,得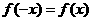 ,即
,即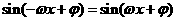 ,
,
展开整理得: ,对任意
,对任意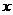 都成立,且
都成立,且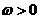 ,所以
,所以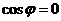 .
.
又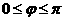 ,所以
,所以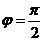 .由
.由 的图象关于点
的图象关于点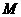 对称,
对称,
得 .
.
取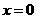 ,得
,得 ,
,
所以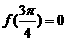 ,∴
,∴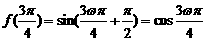 .
.
所以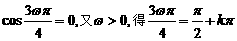 ,
,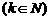 .即
.即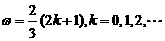
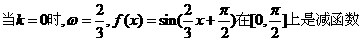 ;
;
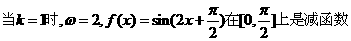 ;
;
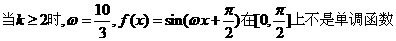 ;
;
综上所得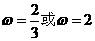 .
.
(二)主要方法:
1.三角函数的奇偶性的判别主要依据定义:首先判定函数的定义域是否关于原点对称,当函数的定义域关于原点对称时,再运用奇偶性定义判别;
2.函数
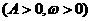 的单调区间的确定,基本思路是把
的单调区间的确定,基本思路是把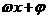 看作一个整体,运用复合函数的单调规律得解;
看作一个整体,运用复合函数的单调规律得解;
3.比较三角函数值的大小,利用奇偶性或周期性转化为属于同一单调区间上的同名函数值,再利用单调性比较大小.
(一)主要知识:
三角函数的奇偶性和单调性具体如下表:
|
函数 |
奇偶性 |
单调区间 |
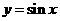 |
奇 |
在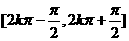 上增 上增在 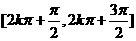 减 减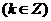 |
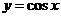 |
偶 |
在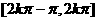 上增 上增在 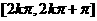 减 减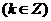 |
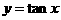 |
奇 |
在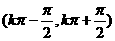 上增 上增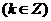 |
|

|
版权所有:()
版权所有:(www..co
(四)巩固练习:
1.已知函数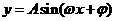 在同一周期内,当
在同一周期内,当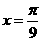 时,取得最大值
时,取得最大值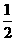 ,当
,当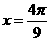 时,取得最小值
时,取得最小值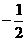 ,则该函数的解析式是
(
,则该函数的解析式是
(  )
)
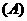
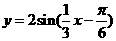

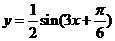

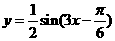
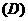
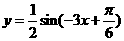
2.若方程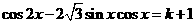 有解,则
有解,则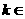
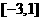 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com