
题目列表(包括答案和解析)
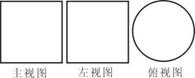
4.如图所示,一个空间几何体的主视图和左视图都是
边长为1的正方形,俯视图是一个直径为1的圆,
那么这个几何体的体积为 ( )
A.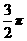 B.
B.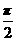 C.
C.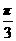 D.
D.
3.若函数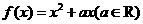 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.存在a∈R,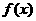 是偶函数
是偶函数
B.存在a∈R,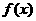 是奇函数
是奇函数
C.对于任意的a∈R,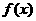 在(0,+∞)上是增函数
在(0,+∞)上是增函数
 D.对于任意的a∈R,
D.对于任意的a∈R,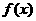 在(0,+∞)上是减函数
在(0,+∞)上是减函数
2.已知复数的实部为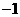 ,虚部为2,则
,虚部为2,则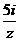 = ( )
= ( )
A.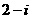 B.
B.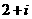 C.
C.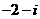 D.
D.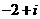
1.已知集合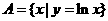 ,集合
,集合 ,则
,则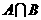 = ( )
= ( )
A.(1,2)
B.{1,2}
C.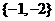 D.
D.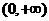
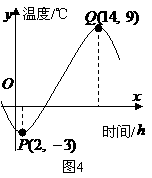 ⒗(本小题满分14分)春节期间,某地昼夜气温呈周期性变化,温度
⒗(本小题满分14分)春节期间,某地昼夜气温呈周期性变化,温度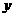 随时间
随时间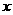 变化近似满足函数
变化近似满足函数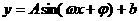 (
(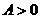 ,
,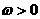 ,
,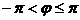 )(如图4),且在每天凌晨
)(如图4),且在每天凌晨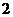 时达到最低温度
时达到最低温度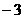 ℃,在下午
℃,在下午 时达到最高温度
时达到最高温度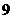 ℃.
℃.
⑴求这段时间气温随时间变化的函数解析式;
⑵这段时间该地一昼夜内哪几个时刻的气温为 ℃?
℃?
注:一昼夜指从凌晨0时(含)到午夜24时(不含).
⒘(本小题满分12分)某地为了建立幸福指标体系,决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
⑴求研究小组的总人数;
|
|
相关人员数 |
抽取人数 |
|
公务员 |
32 |
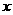 |
|
教师 |
48 |
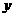 |
|
自由职业者 |
64 |
4 |
⑵若从研究小组的公务员和教师中随机选2人撰写研究报告,求其中恰好有1人来自公务员的概率.
 ⒙(本小题满分14分)如图5,
⒙(本小题满分14分)如图5,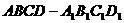 是四棱柱,底面
是四棱柱,底面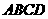 是菱形,
是菱形, 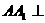 底面
底面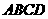 ,
,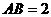 ,
,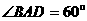 ,
,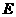 是
是 的中点.
的中点.
⑴求证:平面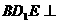 平面
平面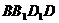 ;
;
⑵若四面体 的体积
的体积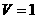 ,
,
求棱柱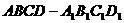 的高.
的高.
⒚(本小题满分12分)已知直线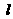 :
: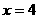 与
与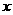 轴相交于点
轴相交于点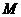 ,
,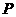 是平面上的动点,满足
是平面上的动点,满足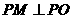 (
( 是坐标原点).
是坐标原点).
⑴求动点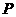 的轨迹
的轨迹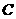 的方程;
的方程;
⑵过直线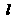 上一点
上一点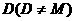 作曲线
作曲线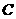 的切线,切点为
的切线,切点为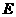 ,与
,与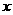 轴相交点为
轴相交点为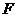 ,若
,若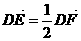 ,求切线
,求切线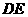 的方程.
的方程.
⒛(本小题满分14分)在平面直角坐标系 中,
中,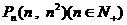 是抛物线
是抛物线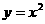 上的点,
上的点,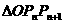 的面积为
的面积为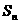 .
.
⑴求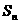 ;
;
⑵化简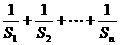 ;
;
⑶试证明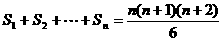 .
.
21(本小题满分14分)设 是函数
是函数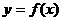 定义域内的一个区间,若存在
定义域内的一个区间,若存在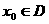 ,使
,使 ,则称
,则称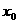 是
是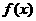 的一个不动点,也称
的一个不动点,也称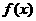 在区间
在区间 上有不动点.
上有不动点.
⑴证明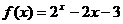 在区间
在区间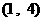 上有不动点;
上有不动点;
⑵若函数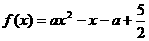 在区间
在区间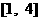 上有不动点,求常数
上有不动点,求常数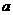 的取值范围.
的取值范围.
(二)选做题(14、15题,考生只能从中选做一题)
⒕(坐标系与参数方程选做题)曲线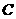 的参数方程是
的参数方程是
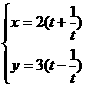 (
(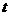 为参数),则曲线
为参数),则曲线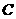 的普通方程是
.
的普通方程是
.
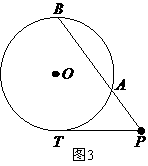
⒖(几何证明选讲选做题)如图3,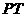 是圆
是圆 的切线,
的切线,
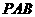 是圆
是圆 的割线,若
的割线,若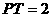 ,
,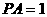 ,
,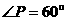 ,
,
则圆 的半径
的半径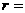 .
.
(一)必做题(11-13题)
⒒若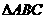 的面积是
的面积是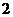 ,
,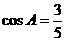 ,则
,则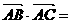 .
.
⒓如图2,程序框图输出的函数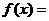 ,值域是 .
,值域是 .
⒔观察下列各式:①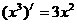 ;②
;②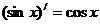 ;
;
③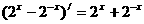 ;④
;④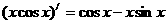
根据其中函数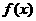 及其导函数
及其导函数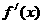 的奇偶性,运用
的奇偶性,运用
归纳推理可得到的一个命题是: .
⒈已知集合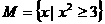 ,下列实数
,下列实数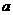 中,符合
中,符合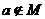 的是
的是
A.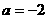 B.
B.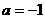 C.
C.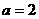 D.
D.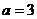
⒉在复平面内,点 、
、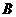 对应的复数分别是
对应的复数分别是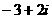 、
、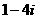 ,则线段
,则线段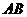 的中点对应的复数是
的中点对应的复数是
A.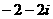 B.
B.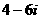 C.
C.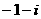 D.
D.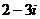
⒊已知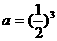 ,
,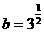 ,
,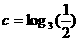 ,则
,则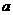 、
、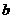 、
、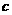 的大小关系是
的大小关系是
A.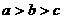 B.
B. C.
C.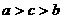 D.
D.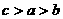
⒋设向量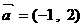 、
、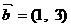 ,下列结论中,正确的是
,下列结论中,正确的是
A.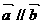 B.
B.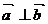 C.
C.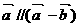 D.
D.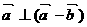
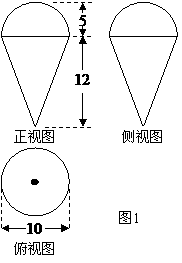 ⒌某型号儿童蛋糕上半部分是半球,下半部分是圆锥,
⒌某型号儿童蛋糕上半部分是半球,下半部分是圆锥,
三视图如图 ,则该型号蛋糕的表面积
,则该型号蛋糕的表面积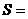
A.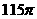 B.
B.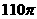
C.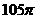 D.
D.
⒍已知椭圆短轴上的两个顶点分别为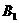 、
、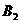 ,焦点
,焦点
为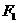 、
、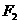 ,若四边形
,若四边形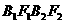 是正方形,则这个
是正方形,则这个
椭圆的离心率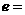
A.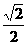 B.
B.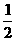 C.
C.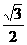 D.以上都不是
D.以上都不是
⒎已知数列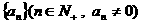 ,则“
,则“ ”是“
”是“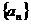 是等比数列”的
是等比数列”的
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.以上都不是
⒏已知平面区域 :
: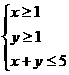 ,
,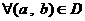 ,
,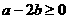 的概率是
的概率是
A.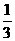 B.
B.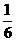 C.
C.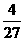 D.
D.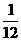
⒐曲线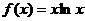 在点
在点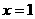 处的切线方程是
处的切线方程是
A.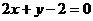 B.
B.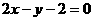 C.
C.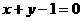 D.
D.
⒑若正实数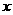 、
、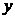 满足
满足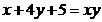 ,则
,则
A.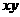 的最小值是25
B.
的最小值是25
B.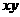 的最大值是25
的最大值是25
C. 的最小值是
的最小值是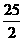 D.
D. 的最大值是
的最大值是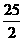
6.(本小题满分10分)
袋中有大小相同的三个球,编号分别为1、2和3,从袋中每次取出一个球,若取到的
球的编号2,则把该球编号改为3后放回袋中继续取球;若取到球的编号为奇数,则取
球停止.用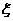 表示所有被取球的编号之和.
表示所有被取球的编号之和.
(1)求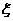 的概率分布;
的概率分布;
(2)求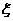 的数学期望与方差.
的数学期望与方差.
说明,证明步骤或演算步骤.
5.(本小题满分10分)
直线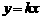 将抛物线
将抛物线 与x轴所围图形分为面积相等的两部分,求
与x轴所围图形分为面积相等的两部分,求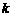 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com