
题目列表(包括答案和解析)
2.(1)若集合P=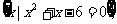 S
S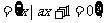 且S
且S P,求a的可取值组成的集合;
P,求a的可取值组成的集合;
(2)若集合A=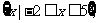 B
B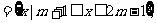 且B
且B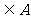 ,求由m的可取值组成的集合.
,求由m的可取值组成的集合.
1.设含有三个实数的集合可表示为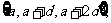 也可表示为
也可表示为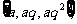 其中a,d,q
其中a,d,q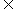 R,求常数q.
R,求常数q.
5.设集合A=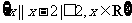 ,B=
,B=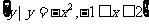 ,则
,则 R(A
R(A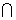 B)= .
B)= .
 例题精讲
例题精讲
例1 若a,b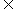 R,集合
R,集合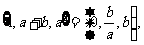 求b-a的值.
求b-a的值.
.
例2 已知集合A=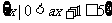 ,集合B=
,集合B=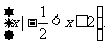
(1)若A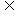 B,求实数a的取值范围;
B,求实数a的取值范围;
(2)若B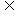 A,求实数a的取值范围;
A,求实数a的取值范围;
(3)A、B能否相等?若能,求出a的值;若不能,试说明理由.
例3(14分)设集合A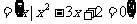 B
B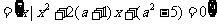
(1)若A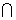 B
B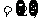 求实数a的值;
求实数a的值;
(2)若A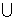 B=A求实数a的取值范围;
B=A求实数a的取值范围;
(3)若U=R,A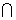 (
( UB)=A.求实数a的取值范围.
UB)=A.求实数a的取值范围.
例4
若集合A1、A2满足A1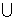 A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)为集合A的同一种分拆,则集合A=
A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)为集合A的同一种分拆,则集合A=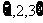 的不同分拆种数是 .
的不同分拆种数是 .
 巩固练习
巩固练习
4.设集合U=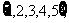 A
A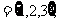 B
B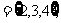 则
则 U(A
U(A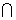 B)等于
.
B)等于
.
3.设全集U={1,3,5,7},集合M={1,|a-5|},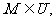
 UM={5,7},则a的值为
.
UM={5,7},则a的值为
.
2.设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是 .
1.满足M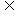
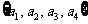 ,且M
,且M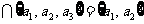 的集合M的个数是
.
的集合M的个数是
.
12.设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠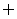 ?若存在,请求出a的值;若不存在,说明理由.
?若存在,请求出a的值;若不存在,说明理由.
解 假设A∩B≠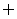 ,则方程组
,则方程组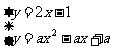 有正整数解,消去y,
有正整数解,消去y,
得ax2-(a+2)x+a+1=0. (*)
由Δ≥0,有(a+2)2-4a(a+1)≥0, 解得-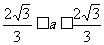 .因a为非零整数,∴a=±1,
.因a为非零整数,∴a=±1,
当a=-1时,代入(*), 解得x=0或x=-1, 而x∈N*.故a≠-1. 当a=1时,代入(*),
解得x=1或x=2,符合题意.故存在a=1,使得A∩B≠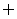 ,此时A∩B={(1,1),(2,3)}
,此时A∩B={(1,1),(2,3)}
11.已知集合A=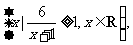 B=
B=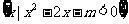
(1)当m=3时,求A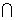 (
( RB);
RB);
(2)若A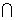 B
B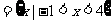 ,求实数m的值.
,求实数m的值.
解
由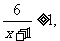 得
得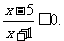 ∴-1<x≤5,∴A=
∴-1<x≤5,∴A=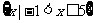 .
.
(1)当m=3时,B=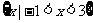 ,则
,则 RB=
RB=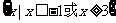 ,
,
∴A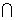 (
( RB)=
RB)=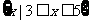 .
.
(2)∵A=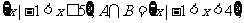 ∴有42-2×4-m=0,解得m=8.
∴有42-2×4-m=0,解得m=8.
此时B=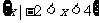 ,符合题意,故实数m的值为8.
,符合题意,故实数m的值为8.
10.(1)已知A={a+2,(a+1)2,a2+3a+3}且1∈A,求实数a的值;
(2)已知M={2,a,b},N={2a,2,b2}且M=N,求a,b的值.
解(1)由题意知:a+2=1或(a+1)2=1或a2+3a+3=1,
∴a=-1或-2或0,根据元素的互异性排除-1,-2, ∴a=0即为所求.
(2)由题意知,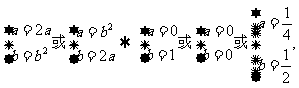
根据元素的互异性得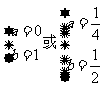 即为所求.
即为所求.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com