
题目列表(包括答案和解析)
5、35% 6、16 7、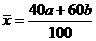 8、
8、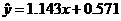
1、D 2、A 3、C 4、B
6、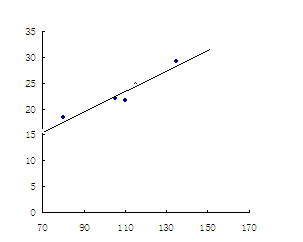 解答:(1)如图所示
解答:(1)如图所示
(2)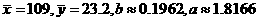 ,
,
所以回归直线方程为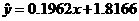 .
.
(3)由(2),当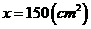 时,为31.2466万元.
时,为31.2466万元.
[拓展探究]
证明:
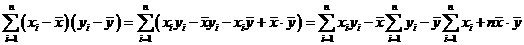
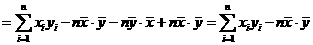 .
.
上式中令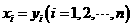 则有恒等式:
则有恒等式: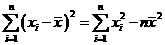
所以得证.
[回顾反思]
求线形回归直线方程的操作步骤是:
第一步:列表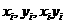 ;第二步:计算:
;第二步:计算: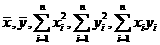 ;
;
第三步:代入公式计算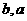 的值;第四步:写出回归方程。
的值;第四步:写出回归方程。
本章测试
1、B 2、C 3、A 4、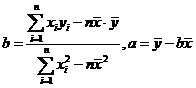 5、
5、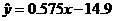
6、解答:列表:
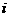 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
 |
-1 |
-2 |
-3 |
-4 |
-5 |
5 |
3 |
4 |
2 |
1 |
 |
-9 |
-7 |
-5 |
-3 |
-1 |
1 |
5 |
3 |
7 |
9 |
 |
9 |
14 |
15 |
12 |
5 |
5 |
15 |
2 |
14 |
9 |
计算得: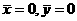 ,
,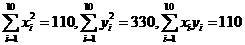 ,
,
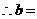
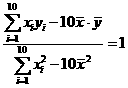 ,
,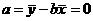 ,所以,回归直线方程为
,所以,回归直线方程为 .
.
[拓展探究]
[回顾反思]
解答:相同点:两者均是指两个变量之间的关系;
不同点:函数关系是一种确定关系,是两个非随机变量的关系,而相关关系是非随机变量与随机变量的关系;函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系。
第12课时
[范例展示]
例1、分析:由题意需作回归分析、先画出其散点图,看其是否呈直线形,然后求出回归直线方程.
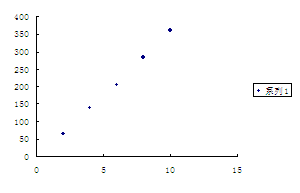 解答:(1)画出其散点图,观察散点图,可以发现5个样本点都落在一条直线附近,所以变量
解答:(1)画出其散点图,观察散点图,可以发现5个样本点都落在一条直线附近,所以变量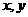 属于线性相关.
属于线性相关.
(2)由于尿汞含量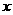 与消光系数
与消光系数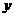 线性相关,可利用公式求得
线性相关,可利用公式求得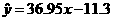 .
.
(3)当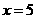 时,
时,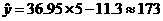 ,可知尿汞含量为
,可知尿汞含量为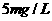 时的消光系数为173.
时的消光系数为173.
例2、分析:把题中的量用回归分析的专用术语改写后在顺着回归分析的一般步骤解题.
解答:(1)用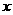 来表示机器速度,
来表示机器速度,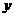 表示每小时生产有问题的物件数,那么4个样本数据为:
表示每小时生产有问题的物件数,那么4个样本数据为:
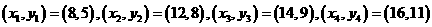 ,则
,则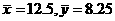
所以,回归直线的斜率为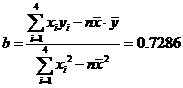 ,
,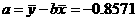 ,
,
所以回归直线方程为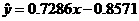
(2)由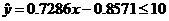 ,
,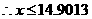 ,所以机器的速度不能超过14.9013转/秒.
,所以机器的速度不能超过14.9013转/秒.
评析:我们在求经验公式后,往往用来做为现实生产中两变量之间相关关系的近似关系,从而可以用来指导生产实践.
[自我测评]
1、C 2、C 3、D 4、A 5、(1)(2)(3)
6、解答:
(1)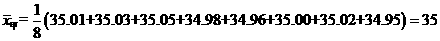 毫米,
毫米,
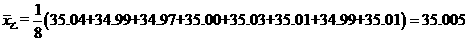 毫米
毫米
(2)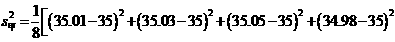
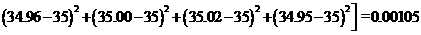 毫米2
毫米2
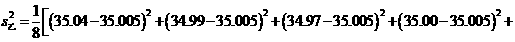
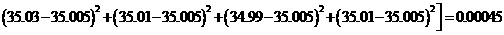
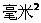
(3)因为,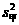 >
>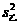 ,所以乙的零件的尺寸更接近于35毫米.
,所以乙的零件的尺寸更接近于35毫米.
[拓展探究]
解答: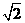
[回顾反思]
解答:如果一组数据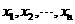 的方差为
的方差为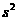 ,则
,则
(1)新数据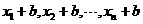 的方差仍为
的方差仍为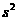
(2)新数据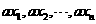 的方差为
的方差为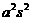
(3)新数据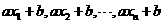 的方差为
的方差为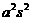
第11课时
 [范例展示]
[范例展示]
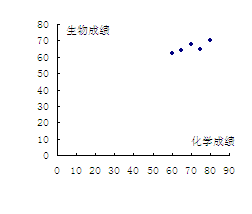
例1、分析:涉及两个变量:化学成绩与生物成绩,可以以化学成绩为自变量,考察因变量生物成绩的变化趋势.
解答:以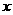 轴表示化学成绩,
轴表示化学成绩,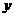 轴表示生物成绩,可得相应的散点图如图所示:
轴表示生物成绩,可得相应的散点图如图所示:
由散点图可见,两者之间具有相关关系.
反思:判断变量间有无相关关系,一种常用的简便可行的方法就是绘制散点图
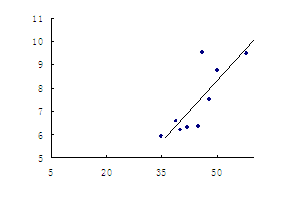
例2、分析:画散点图时,横轴和纵轴的长度单位可以不一致.
解答:(1)如图所示
(2)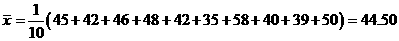
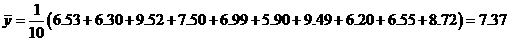
设回归直线的方程为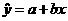 ,则
,则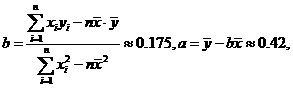
回归直线的方程为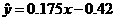 ,回归直线的图形如上图.
,回归直线的图形如上图.
评析:由于横纵轴长度单位不一致,回归直线在图形中的形成和实际情况是不同的.
[自我测评]
1、C 2、C 3、D 4、甲 5、2
6、解答:(1)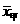 =87,
=87,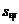 =12.7,
=12.7,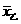 =95,
=95,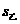 =9.7
=9.7
(2)由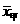 =87<
=87<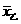 =95,且
=95,且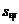 =12.7>
=12.7>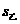 =9.7,故甲的数学学习状况不如乙的数学学习状况.
=9.7,故甲的数学学习状况不如乙的数学学习状况.
[拓展探究]
解答: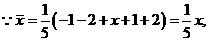
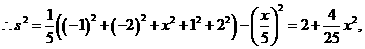
又 且
且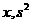 均为整数,
均为整数,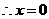 或5.
或5.
当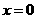 时,
时,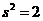 ,所以
,所以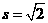 ;当
;当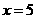 时,
时,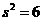 ,所以
,所以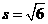 .
.
[回顾反思]
新数据法: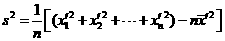 等。
等。
第10课时
[范例展示]
例1、分析:要知道哪种玉米的苗长的高,只要比较甲、乙两种玉米的平均高度即可;要知道哪种玉米的苗长的整齐,只要比较两种玉米苗高的方差大小就可以得到结论.
解答:(1)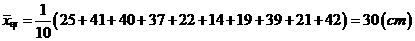 ,
,
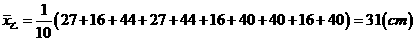 ,
,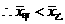 .
.
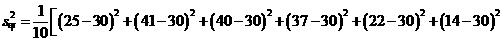 (2)
(2)
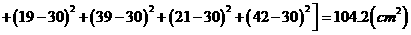
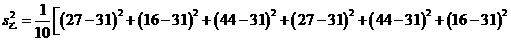
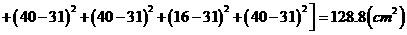
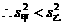 ,所以乙种玉米的苗长的高;甲种玉米的苗长得整齐.
,所以乙种玉米的苗长的高;甲种玉米的苗长得整齐.
评析:比较两组数据平均水平的高低,只需要计算它们的平均数,并比较它们的大小即可,同样,要看两组数据的波动性,只需要计算出它们的方差或标准差,并比较它们的大小即可,但需要注意的是,平均数越大数据平均水平越高;方差或标准差越大,数据的波动越大、稳定性约差.
例2、分析:对照标准差基本公式,先把这两组数据的平均数代数式表示出来,再运用标准差基本公式化简可得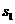 和
和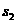 的关系式.
的关系式.
解答:设数据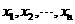 的平均数为
的平均数为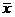 ,即
,即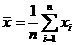 ,设
,设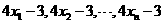 的平均数为
的平均数为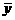 ,即
,即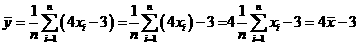 ,
,
所以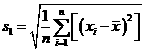 ,
,
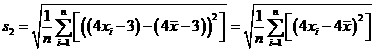
=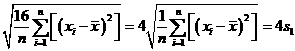 ,所以
,所以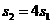 .
.
评析:由本例类似可得如下结论:若把一组数据的每一个数扩大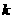 倍并加上一个常数
倍并加上一个常数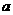 ,则它的标准差扩大
,则它的标准差扩大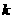 倍,而于常数
倍,而于常数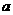 无关.
无关.
[自我测评]
1、A 2、D 3、B 4、2 5、0.065
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com