
题目列表(包括答案和解析)
4.离心率
椭圆的焦距与长轴长的比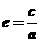 ,叫做椭圆的离心率.∵a>c>0,∴0<e<1.
,叫做椭圆的离心率.∵a>c>0,∴0<e<1.



练习 教科书P.41练习第5题.
例1 求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点的坐标,并用
描点法画出它的图形.
解:把已知方程化成标准方程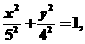 这里a=5,b=4,所以
这里a=5,b=4,所以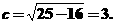
椭圆的长轴和短轴的长分别是2a=10和2b=8,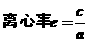 .
.
焦点为F1(-3, 0)、F2(3, 0),顶点是A1(−5,0)、A2(5,0),B1(0,−4)、B2(0,4).
 把已知方程化成标准方程
把已知方程化成标准方程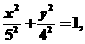

|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
4 |
3.9 |
3.7 |
3.2 |
2.4 |
0 |
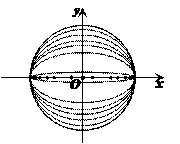
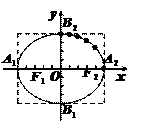
先描点画出椭圆的一部分,再利用椭圆的对称性质画出整个椭圆.
椭圆的简单作法:
(1) 以椭圆的长轴、短轴为邻边画矩形;
(2) 由矩形四边的中点确定椭圆的四个顶点;
(3) 用曲线将四个顶点连成一个椭圆.
例2 求适合下列条件的椭圆的标准方程:
(1) 经过点P(-3, 0)、Q(0,- 2); 
解:(1)由椭圆的几何性质可知,以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点.
即P、Q分别是椭圆长轴和短轴的一个端点. 于是得a=3,b=2.
又因为长轴在x轴上,所以椭圆的标准方程是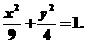
(2) 由已知,2a=20 ,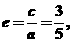 ∴a=10 ,c=6. ∴b2=102-62=64.
∴a=10 ,c=6. ∴b2=102-62=64.
∵椭圆的焦点可能在x轴上,也可能在y轴上,
∴所求椭圆的标准方程为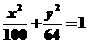
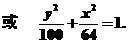
练习 求经过点P (4, 1),且长轴长是短轴长的2倍的椭圆的标准方程.
解:
依题意有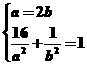 得
得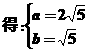
故椭圆方程为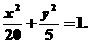
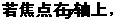


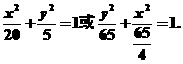
[课后作业]
3.顶点
只须令x=0,得y=±b,点B1(0,-b)、B2(0, b)是椭圆和y轴的两个交点;令y=0,
得x=±a,点A1(-a,0)、A2(a,0)是椭圆和x轴的两个交点.椭圆有四个顶点:A1(-a, 0)、
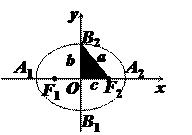 A2(a,
0)、B1(0, -b)、B2(0,
b).椭圆和它的对称轴的四个交点叫椭圆的顶点.
A2(a,
0)、B1(0, -b)、B2(0,
b).椭圆和它的对称轴的四个交点叫椭圆的顶点.
线段A1A2、B1B2分别叫做椭圆的长轴和短轴.
长轴的长等于2a. 短轴的长等于2b.a叫做椭圆的
长半轴长.b叫做椭圆的短半轴长.
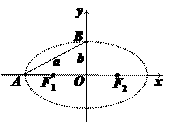
|B1F1|=|B1F2|=|B2F1|=|B2F2|=a.
在Rt△OB2F2中,|OF2|2=|B2F2|2-|OB2|2,
即c2=a2-b2.
小 结 :
由椭圆的范围、对称性和顶点,再进行描点画图,只须描出较少的点,就可以得到较
正确的图形.
2.对称性
在椭圆的标准方程里,把x换成-x,或
把y换成-y,或把x、y同时换成-x、-y时,
方程有变化吗?这说明什么?
椭圆关于y轴、x轴、原点都是对称的.
坐标轴是椭圆的对称轴.
原点是椭圆的对称中心.
椭圆的对称中心叫做椭圆的中心.
1.范围
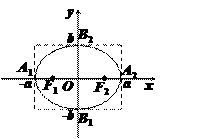 椭圆上点的坐标(x,
y)都适合不等式
椭圆上点的坐标(x,
y)都适合不等式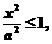
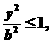 即x2≤a2,y2≤b2,∴|x|≤a,|y|≤b.
即x2≤a2,y2≤b2,∴|x|≤a,|y|≤b.
椭圆位于直线x=±a和y=±b围成的矩形里.
2. 椭圆的标准方程是什么?
[讲授新课]
利用椭圆的标准方程研究椭圆的几何性质.以焦点在x轴上椭圆为例
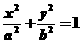 (a>b>0).
(a>b>0).
1. 椭圆的定义是什么?
2.1.2椭圆的简单几何性质(一)
教学目标: 椭圆的范围、对称性、对称中心、离心率及顶点(截距).
重点难点分析
教学重点:椭圆的简单几何性质.
教学难点:椭圆的简单几何性质.
教学设计:
[复习引入]
1.
已知椭圆mx2+5y2=5m的离心率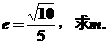
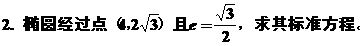
思考 F1、F2 为椭圆的两个焦点,过F2的直线交椭圆于P、Q两点,PF1⊥PQ,且|PF1|=|PQ|,求椭圆的离心率.
[课后作业]
《习案》学案十一,习案十二1、2.
备讲题
例6 已知点M为椭圆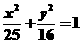 的上任意一点,F1、F2分别为左右焦点; A点坐标为(1,2)
,求
的上任意一点,F1、F2分别为左右焦点; A点坐标为(1,2)
,求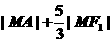 的最小值.
的最小值.
变式1:求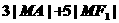 的最小值;
的最小值;
变式2:求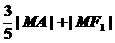 的最小值;
的最小值;
本资料由《七彩教育网》 提供!
2.点P与定点F(2,0)的距离与它到定直线x=2的距离之比为1:2,求点P的轨迹方程.
例3 如图,一种电影放映灯的反射镜面是旋转椭圆面的一部分.过对称的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2.已知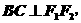
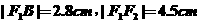 .建立适当的坐标系,求截口BAC所在椭圆的方程.
.建立适当的坐标系,求截口BAC所在椭圆的方程.
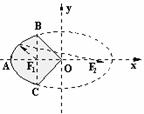
例4如图所示,我国发射的第一颗人造地球卫星运行轨道是以地心(地球的中心)F2为一个焦点的椭圆,已知它的近地点A(离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,并且F2、A、B在同一直线上,地球半径约为6371km,求卫星运行的轨道方程(精确到1km).
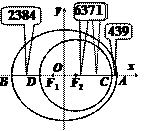
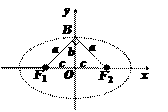 例5 求适合下列条件的椭圆的离心率.
例5 求适合下列条件的椭圆的离心率.
(1) 从短轴端点看两个焦点,所成视角为直角;
(2) 两个焦点间的距离等于长轴的端点与短轴的端点间的距离.
练习3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com