
题目列表(包括答案和解析)
6、函数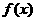 是定义在R上的奇函数,f(x+2)=-f(x),则的值为(
)
是定义在R上的奇函数,f(x+2)=-f(x),则的值为(
)
A. -1 B. 0 C. 1 D. 2
5、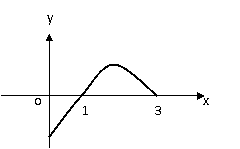 函数
函数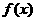 是定义在
是定义在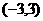 上的奇函数,当
上的奇函数,当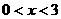 时,
时,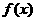 得图像如图所示,那么不等式
得图像如图所示,那么不等式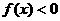 的解集是( )
的解集是( )
(A) 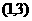 ∪
∪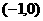 (B)
(B) 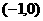 ∪(0,1)
∪(0,1)
(C) (1,3) ∪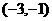 (D)
(D) 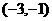 ∪(0,1)
∪(0,1)
4、设偶函数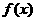 的定义域为R,当
的定义域为R,当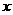
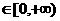 时
时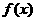 是增函数,则
是增函数,则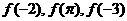 的大小关系是( )
的大小关系是( )
(A)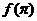 >
>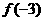 >
>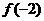 (B)
(B)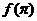 >
>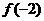 >
>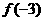
(C)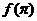 <
<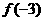 <
<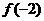 (D)
(D)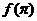 <
<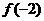 <
<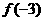
3、若函数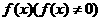 为奇函数,则必有( )
为奇函数,则必有( )
(A)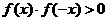 (B)
(B)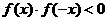
(C)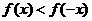 (D)
(D)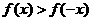
2、函数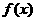 的定义域为
的定义域为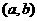 ,且对其内任意实数
,且对其内任意实数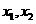 均有:
均有: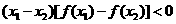 ,则
,则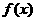 在
在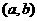 上是( )
上是( )
(A)增函数 (B)减函数
(C)奇函数 (D)偶函数
1、若函数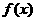 在区间(a,b)上为增函数,在区间(b,c)上也是增函数,则函数
在区间(a,b)上为增函数,在区间(b,c)上也是增函数,则函数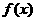 在区间(a,c)上( )
在区间(a,c)上( )
(A)必是增函数 (B)必是减函数
(C)是增函数或是减函数 (D)无法确定增减性
1 单调函数的定义:一般的设 函数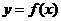 的定义域为A,区间
的定义域为A,区间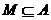 ,
,
2 如果取区间M中的任意两个值X1,X2 ,改变量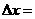 ,当
,当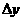 =
时,就称函数
=
时,就称函数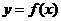 在区间M上是增函数,
在区间M上是增函数,
当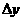 =
时,就称函数
=
时,就称函数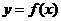 在区间M上是减函数。如果函数
在区间M上是减函数。如果函数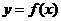 在区间M上是 就说函数
在区间M上是 就说函数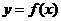
在区间M上具有单调性(区间M称为 )。
3 偶函数的定义:
如果函数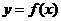 的定义域对于内的 ,都有
,那么称函数
的定义域对于内的 ,都有
,那么称函数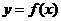 是偶函数.
是偶函数.
4 奇函数的定义:
如果对于函数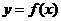 的定义域内的 ,都有 ,那么称函数
的定义域内的 ,都有 ,那么称函数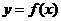 是奇函数.
是奇函数.
5 函数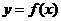 是
,我们就说函数
是
,我们就说函数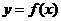 具有奇偶性;
具有奇偶性;
根据奇偶性可将函数分为四类:
奇函数的图像关于 对称,偶函数的图像关于 对称;
奇、偶函数的定义域关于 对称.
11.某人开汽车以 的速度从
的速度从 地到
地到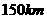 远处的
远处的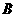 地,在
地,在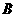 地停留
地停留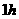 后,再以
后,再以 的速度返回
的速度返回 地,把汽车离开
地,把汽车离开 地的路程
地的路程 表示为时间
表示为时间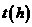 (从
(从 地出发是开始)的函数,并画出函数的图象;再把车速
地出发是开始)的函数,并画出函数的图象;再把车速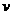
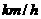 表示为时间
表示为时间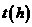 的函数,并画出函数的图象.
的函数,并画出函数的图象.
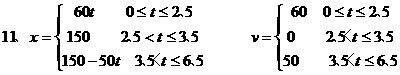
练习题答案:
AABBCC 7、3x+1 8、-3 9、4
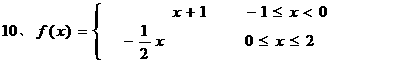
函数的基本性质
8、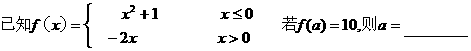
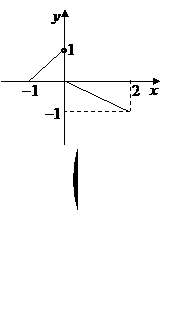
 10.函数在闭区间
10.函数在闭区间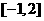 上的图象如右图所示,
上的图象如右图所示,
则求此函数的解析式.
7、已知f(x-2)=3x-5,则f(x)= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com