
题目列表(包括答案和解析)
1、函数的概念:___________________________________
2。了解分段函数的函数,会画比较简单的分段函数的图象。
[知识再现]
1.分段函数的概念。
2.1.2函数的表示方法 学案(2)
[预习要点及要求]
4、开始时水桶甲中有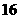 升水,水通过水桶甲的底部小孔流入水桶乙中,
升水,水通过水桶甲的底部小孔流入水桶乙中,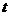 分钟后剩余的水符合指数衰减曲线
分钟后剩余的水符合指数衰减曲线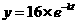 (
(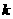 是正常数),假设经过
是正常数),假设经过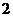 分钟时水桶甲和水桶乙的水量相等,那么经过多少分钟时水桶甲的水剩余2升?
分钟时水桶甲和水桶乙的水量相等,那么经过多少分钟时水桶甲的水剩余2升?
解析:由题意,当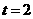 时,
时,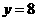 ,即
,即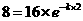 ,故
,故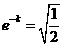 ,
,
设经过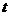 分钟时水桶甲的水剩余2升,则
分钟时水桶甲的水剩余2升,则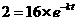 ,
,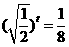 ,
,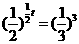 ,
,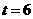
答:经过6分钟时水桶甲的水剩余2升
3、某人骑车沿直线旅行,先前进了a千米,休息了一段时间,又原路返回b千米(0<b<a),
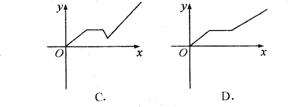
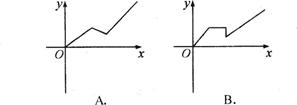 再前进c千米,则此人离起点的距离y与时间x的关系示意图是( ).
再前进c千米,则此人离起点的距离y与时间x的关系示意图是( ).
解析:观察排除法.因“前进了a千米后休息了一段时间”, 排除A;接着“又原路返回b千米(0<b<a),”再排除B,D,应选C
2、某种产品每件80元可售出30件,如果每件定价120元,则每天可售出20件,如果售出件数是定价的一次函数,则这个函数解析式为
解析:设售出件数为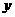 件,定价为
件,定价为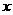 元,则有
元,则有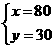 或
或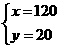 ,设一次函数为
,设一次函数为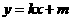 ,则有
,则有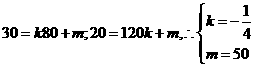 ,因此一次函数为
,因此一次函数为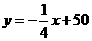 .另因
.另因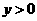 ,则
,则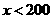 ,又
,又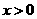 ,因此可得
,因此可得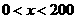 ,即有
,即有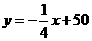 ,
,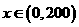 .
.
例4、某工厂转换机制,在两年内生产值的月增长率都是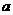 ,则这两年内第二年某月的产值比第一年相应月产值的增长率是多少?
,则这两年内第二年某月的产值比第一年相应月产值的增长率是多少?
错解:设第一年某月的产值为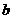 ,则第二年相应月的产值是
,则第二年相应月的产值是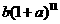 ,依题意所求增长率是
,依题意所求增长率是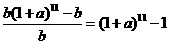 .
.
错解分析:对于增长率问题,主要是应用公式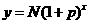 ,对于
,对于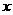 往往指基数所在时间后跨过时间的间隔数.
往往指基数所在时间后跨过时间的间隔数.
正解:不妨设第一年2月份的产值为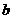 ,则3月份的产值为
,则3月份的产值为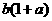 ,4月份的产值为
,4月份的产值为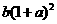 ,依次类推,到第二年2月份是第一年2月份后的第12个月,即一个时间间隔是一个月,这里跨过了12个月,故第二年2月份产值是
,依次类推,到第二年2月份是第一年2月份后的第12个月,即一个时间间隔是一个月,这里跨过了12个月,故第二年2月份产值是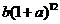 ,又由增长率的概念知,这两年内的第二年某月的产值比第一年相应月的增长率为:
,又由增长率的概念知,这两年内的第二年某月的产值比第一年相应月的增长率为: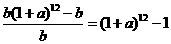 .
.
函数应用问题解题时要掌握好函数应用问题解题的一般步骤,注意避免进入以上两个误区.具体的解题步骤一般有“审题”、“建模”、“求模”、“还原”四步,审题:弄清题意,分清条件结论,理顺数量关系;建模:将文字语言转化成数学语言,用数学知识建立相应的数学模型;求模:求解数学模型,得到数学结论;还原:将用数学方法得到的结论还原为实际问题的意义.
变式练习题
1、已知A、B两地相距150千米,某人开汽车以60千米/小时的速度从A到达B地,在B地停留1小时后再以50千米/小时的速度返回A地,把汽车离开A地的距离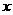 表示为时间
表示为时间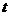 的函数,表达式为
的函数,表达式为
解析:由A到B共用时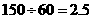 ,停留1小时距离不变,由B返回时距离逐渐减小,
,停留1小时距离不变,由B返回时距离逐渐减小,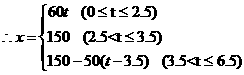
例3、WAP手机上网每月使用量在500分钟以下(包括500分钟),按30元计费;超过500分钟的部分按0.15/分钟计费。假如上网时间过短(小于60分钟的),使用量在1分钟以下不计费,在1分钟以上(包括1分钟)按0.5元/分钟计费。WAP手机上网不收通话费和漫游费。
(1)写出上网时间x分钟与所付费用y元之间的函数关系式;
(2)12月小王WAP上网使用量为20小时,要付多少钱?
(3)小王10月份付了90元的WAP上网费,那么他上网的时间是多少?
错解:1)设上网时间为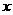 分钟,由已知条件所付费用
分钟,由已知条件所付费用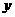 关于
关于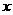 的函数关系式为
的函数关系式为
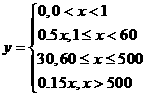
(2)当 分钟,
分钟,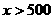 ,应付
,应付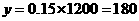 元,
元,
(3)90元已超过30元,所以上网时间超过500分钟,由解析式可得上网时间为600分钟。
错解分析:此题错解主要是对“超过500分钟的部分按0.15/分钟计费”中的“超过部分”理解出错,产生了与事实相违的结论,如第(2)小题上了1200分钟的网,要180元,是30元包月用500分钟的6倍,而时间上才2倍多,与事实不符;又如第(3)小题,用了90元,几乎是30元的3倍,而可上网时间才多了100分钟,与事实不符.
正解:(1)设上网时间为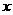 分钟,由已知条件所付费用
分钟,由已知条件所付费用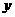 关于
关于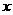 的函数关系式为
的函数关系式为
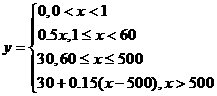 (2)当
(2)当 分钟,
分钟,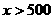 ,应付
,应付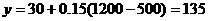 元,
元,
(3)90元已超过30元,所以上网时间超过500分钟,由解析式可得上网时间为900分钟。
例2、在一个交通拥挤及事故易发路段,为了确保交通安全,交通部门规定,在此路段内的车速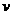 (单位:
(单位: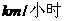 )的平方和车身长(单位:
)的平方和车身长(单位: )的乘积与车距成正比,且最小车距不得少于半个车身长.假定车身长为
)的乘积与车距成正比,且最小车距不得少于半个车身长.假定车身长为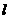 (单位:
(单位: ),且当车速为
),且当车速为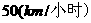 时,车距恰为车身长,问交通繁忙时应规定怎样的车速,才能在此路段的车流量
时,车距恰为车身长,问交通繁忙时应规定怎样的车速,才能在此路段的车流量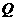 最大?
最大?

错解: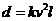 ,将
,将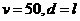 代入得
代入得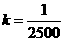 ,
,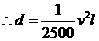 ,又将
,又将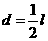 代入得
代入得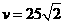 ,由题意得
,由题意得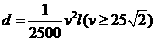 ,
,
将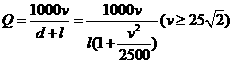 ,
,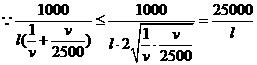
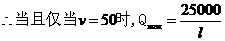
综上所知: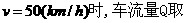 取最大值.
取最大值.
错因分析:上述解法中的结果虽然正确,但解题过程中是错误的,即虽然车速要求不低于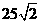
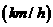 ,所以在求解过程中应分此两种情况分类求解,得到分段函数.
,所以在求解过程中应分此两种情况分类求解,得到分段函数.
正解:依题意,得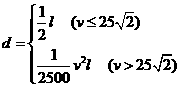 ,
,
则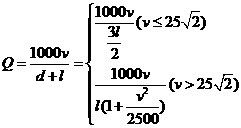 ,显然,当
,显然,当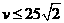 时,
时,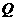 是
是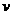 的增函数,
的增函数,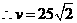 时,
时,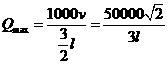 ,
,
当 时,
时,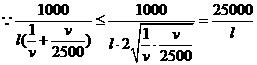 ,当且仅当
,当且仅当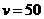 时,
时,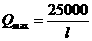 ,综上所述,当
,综上所述,当 时车流量Q取到最大值.
时车流量Q取到最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com